题目内容
过点M（3，0）作直线l与圆：x2+y2=16交于A，B两点，求l的斜率，使△AOB面积最大，并求此最大面积．
解：要使△AOB面积最大，则应有∠AOB=90°，此时O到直线AB的距离d=
=2
．
又直线AB的方程y=k（x-3），
∴
∴k=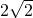
．
此时三角形△AOB面积有最大值8．
分析：判断三角形面积最大值时，∠AOB=90°，利用点到直线的距离求出直线方程的斜率k，然后求出面积的最大值．
点评：本题考查直线与圆的位置关系，点到直线的距离公式的应用，考查计算能力．
=2．又直线AB的方程y=k（x-3），
∴
∴k=
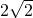．此时三角形△AOB面积有最大值8．
分析：判断三角形面积最大值时，∠AOB=90°，利用点到直线的距离求出直线方程的斜率k，然后求出面积的最大值．
点评：本题考查直线与圆的位置关系，点到直线的距离公式的应用，考查计算能力．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
相关题目
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．