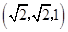题目内容
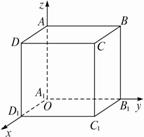
如图,建立空间直角坐标系 D—xyz,已知正方体ABCD—A1B1C1D1的棱长为1,点P是正方体对角线D1B的中点,点Q在棱CC1上.
(1)当2|![]() |=|
|=|![]() |时,求|
|时,求|![]() |;
|;
(2)当点Q在棱CC1上移动时,求|![]() |的最小值.
|的最小值.
解:由题意知:点C1(0,1,1),点C(0,1,0),点P是体对角线D1B的中点,则P(![]() ,
,![]() ,
,![]() ).
).
(1)点Q在棱CC1上,当2|![]() |=|
|=|![]() |时,点Q(0,1,23),
|时,点Q(0,1,23),
∴![]() =(-
=(-![]() ,
,![]() ,
,![]() ),∴|PQ|=
),∴|PQ|=![]() .
.
(2)当点Q在棱CC1上移动时,则点Q(0,1,a)a∈[0,1],![]() =(-
=(-![]() ,
,![]() ,a-
,a-![]() ),
),
∴|![]() |=
|=![]() .
.
当a=![]() 时,|PQ|取得最小值
时,|PQ|取得最小值![]() ,此时Q(0,1,
,此时Q(0,1,![]() ).
).

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 中,
中, ,
, ,
, ,且
,且 两两垂直,
两两垂直, 是
是 中点,
中点, 是
是 重心,现如图建立空间直角坐标系
重心,现如图建立空间直角坐标系 。
。 和
和 所成角的余弦值。
所成角的余弦值。
 中,
中, ,
, ,
, ,且
,且 两两垂直,
两两垂直, 是
是 中点,
中点, 是
是 重心,现如图建立空间直角坐标系
重心,现如图建立空间直角坐标系 。
。 和
和 所成角的余弦值。
所成角的余弦值。
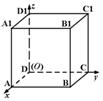
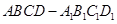 的顶点D为坐标原点O,如图建立空间直角坐标系,则与
的顶点D为坐标原点O,如图建立空间直角坐标系,则与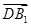 共线的向量的坐标可以是
共线的向量的坐标可以是 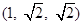 B.
B.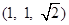
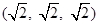 D.
D.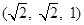
 的顶点D为坐标原点O,如图建立空间直角坐标系,则与
的顶点D为坐标原点O,如图建立空间直角坐标系,则与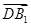 共线的向量的坐标可以是
共线的向量的坐标可以是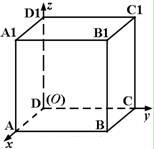
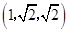 B.
B. C.
C. D.
D.