题目内容
 (2012•黄州区模拟)中国黄石第三届国际矿冶文化旅游节将于2012年8月20日在黄石铁山举行,为了搞好接待工作,组委会准备在湖北理工学院和湖北师范学院分别招募8名和12名志愿者,将这20名志愿者的身高编成如图茎叶图(单位:cm)
(2012•黄州区模拟)中国黄石第三届国际矿冶文化旅游节将于2012年8月20日在黄石铁山举行,为了搞好接待工作,组委会准备在湖北理工学院和湖北师范学院分别招募8名和12名志愿者,将这20名志愿者的身高编成如图茎叶图(单位:cm)若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有湖北师范学院的“高个子”才能担任“兼职导游”.
(1)根据志愿者的身高编茎叶图指出湖北师范学院志愿者身高的中位数;
(2)如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(3)若从所有“高个子”中选3名志愿者,用ξ表示所选志愿者中能担任“兼职导游”的人数,试写出的分布列,并求ξ的数学期望.
分析:(1)根据志愿者的身高编成的茎叶图知湖北师范学院志愿者身高的中位数为168、169的平均数;
(2)由茎叶图可知,“高个子”有8人,“非高个子”有12人,从而可得5人中“高个子”为2人,“非高个子”为3人,从而可求至少有1人为高个子的概率;
(3)确定ξ的可能取值,求出相应的概率,可得ξ的分布列与数学期望.
(2)由茎叶图可知,“高个子”有8人,“非高个子”有12人,从而可得5人中“高个子”为2人,“非高个子”为3人,从而可求至少有1人为高个子的概率;
(3)确定ξ的可能取值,求出相应的概率,可得ξ的分布列与数学期望.
解答:解:(1)根据志愿者的身高编成的茎叶图知湖北师范学院志愿者身高的中位数为:
=168.5.…(2分)
(2)由茎叶图可知,“高个子”有8人,“非高个子”有12人,
∴按照分层抽样抽取的5人中“高个子”为5×
=2人,“非高个子”为5×
=3人,
则至少有1人为高个子的概率P=1-
=
…(6分)
(3)由题可知:湖北师范学院的高个子只有3人,则ξ的可能取值为0,1,2,3;
故P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
,P(ξ=3)=
=
,
即ξ的分布列为:
Eξ=0×
+1×
+2×
+3×
=
. …(12分)
| 168+169 |
| 2 |
(2)由茎叶图可知,“高个子”有8人,“非高个子”有12人,
∴按照分层抽样抽取的5人中“高个子”为5×
| 8 |
| 20 |
| 12 |
| 20 |
则至少有1人为高个子的概率P=1-
| ||
|
| 7 |
| 10 |
(3)由题可知:湖北师范学院的高个子只有3人,则ξ的可能取值为0,1,2,3;
故P(ξ=0)=
| ||
|
| 10 |
| 56 |
| ||||
|
| 30 |
| 56 |
| ||||
|
| 15 |
| 56 |
| ||
|
| 1 |
| 56 |
即ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 10 |
| 56 |
| 30 |
| 56 |
| 15 |
| 56 |
| 1 |
| 56 |
| 9 |
| 8 |
点评:本题考查茎叶图,考查概率的求解,考查离散型随机变量的分布列与数学期望,确定变量的取值,求出相应的概率是关键.

练习册系列答案
相关题目
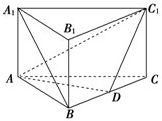 (2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点.
(2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点. (2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为
(2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为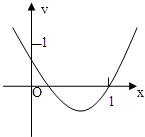 (2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )
(2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )