题目内容
19.如图,正四棱柱ABCD-A1B
(1)求证:平面B1EF⊥平面BDD1B1;
(2)求点D1到平面B1EF的距离d;
(3)求三棱锥B1-EFD1的体积V.
19.
(1)证法一:连结AC.
∵正四棱柱ABCD-A1B
∴AC⊥BD,又AC⊥D1D,故AC⊥平面BDD1B1.
∵E、F分别为AB、BC的中点,故EF∥AC,
∴EF⊥平面BDD1B1,
∴平面B1EF⊥平面BDD1B1.
证法二:∵BE=BF,∠EBD=∠FBD=45°,
∴EF⊥BD.
又EF⊥D1D,
∴EF⊥平面BDD1B1,
∴平面B1EF⊥平面BDD1B1.
(2)在对角面BDD1B1中,作D1H⊥B
∵平面B1EF⊥平面BDD1B1,且平面B1EF∩平面BDD1B1=B
∴D1H⊥平面B1EF,且垂足为H,
∴点D1到平面B1EF的距离d=D1H.

解法一:在Rt△D1HB1中,D1H=D1B1·sinD1B1H.
∵D1B1=![]() A1B1=
A1B1=![]() ·2
·2![]() =4,
=4,
sinD1B1H=sinB1GB=![]() ,
,
∴d=D1H=4·![]() .
.
解法二:∵△D1HB1∽△B1BG,
∴![]() ,
,
∴d=D1H=![]() .
.

解法三:连结D
即![]() ·B
·B![]() B1B2,
B1B2,
∴d=D1H=![]() .
.
(3)V=V![]() =V
=V![]() =
=![]() ·d·
·d·![]() =
=![]() ·
·![]() ·
·![]() ·2·
·2·![]() =
=![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
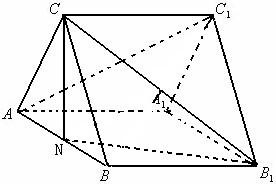 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
