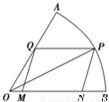
题目内容
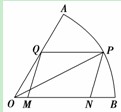
如图,现在要在一块半径为1m.圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ,使点P在AB弧上,点Q在OA上,点M,N在OB上,设∠BOP=θ,的面积为S.
(1)求S关于θ的函数关系式;
(2)求S的最大值及相应θ的值![]() .
. 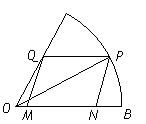
解:在△OPQ中, ![]() =
=![]() =
=![]() =
=![]()
∴ OQ=![]() sinθ,PQ=
sinθ,PQ=![]() sin(60º-θ)
sin(60º-θ)
∴SYMNPQ=2S△OPQ=OQ·PQ·sin120º=![]() sinθ·sin(60º-θ)=
sinθ·sin(60º-θ)=![]() cos(2θ-60º)-
cos(2θ-60º)-![]()
∵0<θ<60º∴-60º<2θ-60º<60º∴![]() <cos(2θ-60º)≤1∴0<SYMNPQ≤
<cos(2θ-60º)≤1∴0<SYMNPQ≤![]()
∴θ=30º时,S的最大值为![]()

练习册系列答案
相关题目
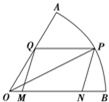 如图,现在要在一块半径为1m.圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ,使点P在AB弧上,点Q在OA上,点M,N在OB上,设∠BOP=θ.平行四边形MNPQ的面积为S.
如图,现在要在一块半径为1m.圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ,使点P在AB弧上,点Q在OA上,点M,N在OB上,设∠BOP=θ.平行四边形MNPQ的面积为S.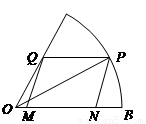
 的
的 的函数关系式;
的函数关系式;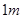 ,圆心角为
,圆心角为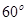 的扇形纸板
的扇形纸板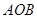 上剪出一个平行四边形
上剪出一个平行四边形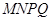 ,使点
,使点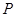 在弧
在弧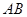 上,点
上,点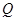 在
在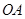 上,点
上,点 ,
, 在
在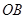 上,设
上,设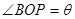 ,
, .
. 
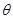 的函数关系式;
的函数关系式;