题目内容
设函数f(x)=x3,若0≤θ≤![]() 时,f(mcosθ)+f(1-m)>0恒成立,则实数m的取值范围为( )
时,f(mcosθ)+f(1-m)>0恒成立,则实数m的取值范围为( )
(A)(-∞,1) (B)(-∞,![]() )
)
(C)(-∞,0) (D)(0,1)
A.因为f(x)=x3为奇函数且在R上为单调增函数,
∴f(mcosθ)+f(1-m)>0⇒f(mcosθ)>f(m-1)
⇒mcosθ>m-1⇒mcosθ-m+1>0恒成立,
令g(cosθ)=mcosθ-m+1,
又0≤θ≤![]() ,∴0≤cosθ≤1,
,∴0≤cosθ≤1,
则有:![]() ,即
,即![]() ,解得:m<1.
,解得:m<1.

练习册系列答案
相关题目
 x3-
x3- x2+a x.
x2+a x.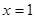 处的切线方程为12x+y-1=0.
处的切线方程为12x+y-1=0. 上的最大值和最小值.
上的最大值和最小值.