题目内容
已知函数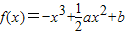 .
.(1)若y=f(x)在x=1处的极值为
 ,求y=f(x)的解析式并确定其单调区间;
,求y=f(x)的解析式并确定其单调区间;(2)当x∈(0,1]时,若y=f(x)的图象上任意一点处的切线的倾斜角为θ,求当
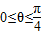 时a的取值范围.
时a的取值范围.
【答案】分析:(1)因为函数在x=1处的极值为 ,所以在在x=1处的导数等于0,且在x=1处的函数值为
,所以在在x=1处的导数等于0,且在x=1处的函数值为 ,就可得到两个关于a,b的等式,解出a,b求出函数的解析式.再列表判断函数在那个范围内导数大于0,即为增区间,在那个范围内导数小于0,即为减区间.
,就可得到两个关于a,b的等式,解出a,b求出函数的解析式.再列表判断函数在那个范围内导数大于0,即为增区间,在那个范围内导数小于0,即为减区间.
(2)因为切线的斜率是倾斜角的正切值,所以当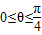 时,0≤k≤1,而切线的斜率又是函数在切点处的导数,所以当x∈(0,1]时,f(x)的图象上任意一点处的导数属于[0,1],这样就可得到含参数a的不等式0≤-3x2+ax≤1在x∈(0,1]上恒成立,再据此求出参数a的范围.
时,0≤k≤1,而切线的斜率又是函数在切点处的导数,所以当x∈(0,1]时,f(x)的图象上任意一点处的导数属于[0,1],这样就可得到含参数a的不等式0≤-3x2+ax≤1在x∈(0,1]上恒成立,再据此求出参数a的范围.
解答:解:(1)f′(x)=-3x2+ax,由题意知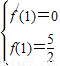
∴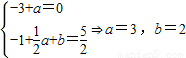 ,
,
∴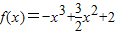
∴f′(x)=-3x2+3x=-3x(x-1),可得函数的单调性如下表
∴f(x)的递增区间为(0,1),递减区间为(-∞,0)及(1,+∞)
(2)∵tanθ=-3x2+ax,
∴0≤-3x2+ax≤1在x∈(0,1]上恒成立,
当0≤-3x2+ax时,可得a≥3x,∴a≥3
当-3x2+ax≤1时,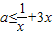 ,
,
又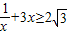 (当且仅当
(当且仅当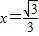 时取等号),∴
时取等号),∴ ,
,
综合得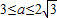
点评:本题主要考查导数在求函数极值,单调区间中的应用,导数的几何意义,以及直线的倾斜角与斜率之间的关系.
 ,所以在在x=1处的导数等于0,且在x=1处的函数值为
,所以在在x=1处的导数等于0,且在x=1处的函数值为 ,就可得到两个关于a,b的等式,解出a,b求出函数的解析式.再列表判断函数在那个范围内导数大于0,即为增区间,在那个范围内导数小于0,即为减区间.
,就可得到两个关于a,b的等式,解出a,b求出函数的解析式.再列表判断函数在那个范围内导数大于0,即为增区间,在那个范围内导数小于0,即为减区间.(2)因为切线的斜率是倾斜角的正切值,所以当
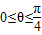 时,0≤k≤1,而切线的斜率又是函数在切点处的导数,所以当x∈(0,1]时,f(x)的图象上任意一点处的导数属于[0,1],这样就可得到含参数a的不等式0≤-3x2+ax≤1在x∈(0,1]上恒成立,再据此求出参数a的范围.
时,0≤k≤1,而切线的斜率又是函数在切点处的导数,所以当x∈(0,1]时,f(x)的图象上任意一点处的导数属于[0,1],这样就可得到含参数a的不等式0≤-3x2+ax≤1在x∈(0,1]上恒成立,再据此求出参数a的范围.解答:解:(1)f′(x)=-3x2+ax,由题意知
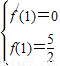
∴
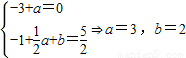 ,
,∴
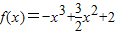
∴f′(x)=-3x2+3x=-3x(x-1),可得函数的单调性如下表
| x | (-∞,0) | (0,1) | 1 | (1,+∞) | |
| f′(x) | - | + | - | ||
| f(x) | 递减 | 递增 | 递减 |
(2)∵tanθ=-3x2+ax,
∴0≤-3x2+ax≤1在x∈(0,1]上恒成立,
当0≤-3x2+ax时,可得a≥3x,∴a≥3
当-3x2+ax≤1时,
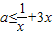 ,
,又
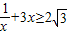 (当且仅当
(当且仅当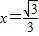 时取等号),∴
时取等号),∴ ,
,综合得
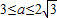
点评:本题主要考查导数在求函数极值,单调区间中的应用,导数的几何意义,以及直线的倾斜角与斜率之间的关系.

练习册系列答案
相关题目
 ,
,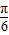 个单位后,再将得到的函数图象上的各点横坐标伸长到原来的2倍,得到函数g(x),若
个单位后,再将得到的函数图象上的各点横坐标伸长到原来的2倍,得到函数g(x),若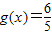 ,求
,求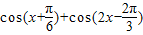 的值.
的值.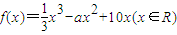 .
. .
.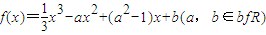 .
.