题目内容
在正方体ABCD-A1B1C1D1中，直线A1B与平面BC1D1所成的角为
- A.arctan
- B.
- C.
- D.
B
分析：建立空间直角坐标系，求出平面BC1D1的法向量，利用公式求出直线A1B与平面BC1D1所成的角．
解答：
解：如图建立空间直角坐标系，设棱长为1，
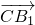是平面BC1D1的法向量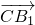，=（0，1，1）
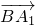=（-1，0，1）
直线A1B与平面BC1D1所成的角为α
sinα=
所以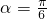
故选B．
点评：本题考查用空间向量求直线与平面的夹角，考查逻辑思维能力，计算能力，是基础题．
分析：建立空间直角坐标系，求出平面BC1D1的法向量，利用公式求出直线A1B与平面BC1D1所成的角．
解答：
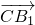解：如图建立空间直角坐标系，设棱长为1，是平面BC1D1的法向量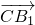，=（0，1，1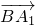）=（-1，0，1）直线A1B与平面BC1D1所成的角为α
sinα=
所以
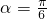
故选B．
点评：本题考查用空间向量求直线与平面的夹角，考查逻辑思维能力，计算能力，是基础题．
练习册系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）