题目内容
已知 ,
, 是两个非零向量,当
是两个非零向量,当 +t
+t (t∈R)的模取最小值时,
(t∈R)的模取最小值时,①求t的值.
②已知
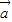 与
与 共线且同向,求证:
共线且同向,求证: 与
与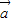 +t
+t 垂直.
垂直.
【答案】分析:①令m=| +t
+t |,
|, ,
, 夹角为θ,对m2进行变形,然后利用二次函数的性质可得其取最小值时t的值;
夹角为θ,对m2进行变形,然后利用二次函数的性质可得其取最小值时t的值;
②当 与
与 共线且同向时,cosθ=1,只需证明
共线且同向时,cosθ=1,只需证明 •(
•( +t
+t )=0即可;
)=0即可;
解答:解:①令m=| +t
+t |,
|, ,
, 夹角为θ,
夹角为θ,
则 •t
•t
=
= +
+ -
- =
= ,
,
所以当t=- 时,
时, ;
;
②证明:因为 与
与 共线且同向,所以cosθ=1,
共线且同向,所以cosθ=1,
所以t=- ,
,
所以 =
= ,
,
所以 .
.
点评:本题考查利用平面向量的数量积证明向量垂直,属基础题.
 +t
+t |,
|, ,
, 夹角为θ,对m2进行变形,然后利用二次函数的性质可得其取最小值时t的值;
夹角为θ,对m2进行变形,然后利用二次函数的性质可得其取最小值时t的值;②当
 与
与 共线且同向时,cosθ=1,只需证明
共线且同向时,cosθ=1,只需证明 •(
•( +t
+t )=0即可;
)=0即可;解答:解:①令m=|
 +t
+t |,
|, ,
, 夹角为θ,
夹角为θ,则
 •t
•t=

=
 +
+ -
- =
= ,
,所以当t=-
 时,
时, ;
;②证明:因为
 与
与 共线且同向,所以cosθ=1,
共线且同向,所以cosθ=1,所以t=-
 ,
,所以
 =
= ,
,所以
 .
.点评:本题考查利用平面向量的数量积证明向量垂直,属基础题.

练习册系列答案
相关题目
 ,
, 是两个非零向量,且|
是两个非零向量,且| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角大小为 .
的夹角大小为 . 、
、 是两个非零向量,且满足|
是两个非零向量,且满足| |=|
|=| |=|
|=| -
- |,求:
|,求: 与
与 +
+ 的夹角;
的夹角; 的值.
的值.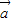 ,
,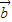 是两个非零向量,且
是两个非零向量,且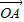 =
=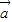 +
+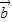 ,
,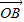 =
=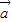 +2
+2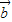 ,
,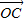 =
=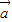 +3
+3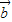 ,则
,则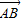 与
与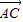 的夹角为 .
的夹角为 .