题目内容
函数 图象的一条对称轴是 ( )
图象的一条对称轴是 ( )
A. | B. | C. | D. |
C
解析试题分析:根据题意,由于正弦函数的对称轴方程为x= ,因此可知函数
,因此可知函数 图像的对称轴方程为
图像的对称轴方程为 ,然后对于k令值可知,当k=0时,则可知
,然后对于k令值可知,当k=0时,则可知 是函数
是函数 图象的一条对称轴,故选C.
图象的一条对称轴,故选C.
考点:对称轴方程
点评:主要是考查了三角函数的对称轴方程的求解,属于基础题。

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
函数 的部分图象如图所示,点
的部分图象如图所示,点 、
、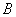 是最高点,点
是最高点,点 是最低点.若△
是最低点.若△ 是直角三角形,则
是直角三角形,则 的值为( )
的值为( )
A. | B. |
C. | D. |
 中,三内角
中,三内角 成等差数列,则
成等差数列,则 的最大值为 ( )
的最大值为 ( )
A. | B. | C. | D.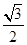 |
为得到函数 的图象,只需将函数
的图象,只需将函数 的图像
的图像
A.向左平移 个长度单位 个长度单位 | B.向右平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
为了得到函数 的图像,只需将函数
的图像,只需将函数 的图像( )
的图像( )
A.向左平移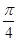 个长度单位 个长度单位 | B.向右平移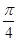 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
设 是定义域为
是定义域为 ,最小正周期为
,最小正周期为 的函数。若
的函数。若 , 则
, 则 等于( )
等于( )
| A.1 | B. | C.0 | D. |
有以下四种变换方式:
向左平行移动 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的 ;
;
向右平行移动 个单位长度,再将每个点的横坐标缩短为原来的
个单位长度,再将每个点的横坐标缩短为原来的 ;
;
每个点的横坐标缩短为原来的 ,再向右平行移动
,再向右平行移动 个单位长度;
个单位长度;
每个点的横坐标缩短为原来的 ,再向左平行移动
,再向左平行移动 个单位长度.
个单位长度.
其中能将函数 的图象变为函数
的图象变为函数 的图象的是( )
的图象的是( )
| A.①和④ | B.①和③ | C.②和④ | D.②和③ |
函数y=cos( -2x)的单调递增区间是 ( )
-2x)的单调递增区间是 ( )
A.[k + + ,kπ+ ,kπ+  ] ] | B.[k - -  ,k ,k + + ] ] |
C.[2k + + ,2k ,2k + +  ] ] | D.[2k - -  ,2kπ+ ,2kπ+ ](以上k∈Z) ](以上k∈Z) |
若 ,则
,则 的取值范围是
的取值范围是
A. |
B. |
C. |
D. |