题目内容
函数y=
（x≥0）的最大值与最小值情况是（ ）A．有最大值为8，无最小值
B．有最大值为8，最小值为4
C．无最大值，有最小值为
D．无最大值，有最小值为4
【答案】分析：y=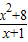
=
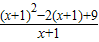=（x+1）+
，由于x≥0，应用基本不等式可得：（x+1）+
≥6-2=4，（当且仅当x=2时取“=”），y有最小值，无最大值，从而得到选项．
解答：解：∵x≥0
∴y=
=
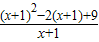=（x+1）+
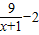≥2
-2=4，（当且仅当x=2时取“=”）
∴函数y=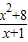
（x≥0）无最大值，有最小值4．
故选D．
点评：本题考查基本不等式，关键在于将y=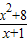
转化为y=（x+1）+
，再应用基本不等式即可，属于中档题．
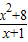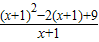==（x+1）+，由于x≥0，应用基本不等式可得：（x+1）+≥6-2=4，（当且仅当x=2时取“=”），y有最小值，无最大值，从而得到选项．解答：解：∵x≥0
∴y=
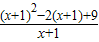==（x+1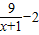）+≥2-2=4，（当且仅当x=2时取“=”）∴函数y=
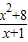（x≥0）无最大值，有最小值4．故选D．
点评：本题考查基本不等式，关键在于将y=
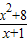转化为y=（x+1）+，再应用基本不等式即可，属于中档题． 
练习册系列答案
阅读快车系列答案
相关题目
（2012•荆州模拟）如上图，函数
的图象如图，f(x)=6lnx+h(x)
)上是单调函数，求实数m的取值范围；
（x≥0）的反函数为（ ）
（x∈R）
（x≥0）
的图象如图，f(x)=6lnx+h(x).
)上是单调函数，求实数m的取值范围；
（x≥0）的反函数为（ ）
（x∈R）
（x≥0）