题目内容
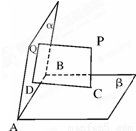
如图，已知平面α∩平面β=AB，PQ⊥α于Q，PC⊥β于C，CD⊥α于D．（1）求证：P、C、D、Q四点共面；
（2）求证：QD⊥AB．
【答案】分析：（1）利用线面垂直的性质，可得线线平行，从而可得四点共面；
（2）利用线面垂直可得线线垂直，再利用线面垂直的判定可得线线垂直．
解答：证明：（1）∵PQ⊥α，CD⊥α，∴PQ∥CD，∴P，C，D，Q四点共面；
（2）设P，C，D，Q四点共面于γ
∵AB?α，PQ⊥α，∴PQ⊥AB，
又∵PC⊥β，AB?β，∴PC⊥AB，
∵PQ∩PC=P，∴AB⊥γ，
又∵QD?γ，∴AB⊥QD
点评：本题考查线面垂直的判定与性质，考查四点共面，掌握线面垂直的判定与性质是关键．
（2）利用线面垂直可得线线垂直，再利用线面垂直的判定可得线线垂直．
解答：证明：（1）∵PQ⊥α，CD⊥α，∴PQ∥CD，∴P，C，D，Q四点共面；
（2）设P，C，D，Q四点共面于γ
∵AB?α，PQ⊥α，∴PQ⊥AB，
又∵PC⊥β，AB?β，∴PC⊥AB，
∵PQ∩PC=P，∴AB⊥γ，
又∵QD?γ，∴AB⊥QD
点评：本题考查线面垂直的判定与性质，考查四点共面，掌握线面垂直的判定与性质是关键．
练习册系列答案
相关题目
9、如图，已知四边形ABCD是平行四边形，点P是平面ABCD外的一点，则在四棱锥P-ABCD中，M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH．
如图，已知直角梯ACDE所在的平面垂直于平ABC，∠BAC=∠ACD=90°，∠EAC=60°，AB=AC=AE．
