题目内容
设f(z)=2z(cos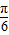 +icos
+icos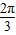 ),这里z是复数,用A表示原点,B表示f (1+
),这里z是复数,用A表示原点,B表示f (1+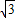 i)所对应的点,C表示点-4i所对应的点,则∠ABC= .
i)所对应的点,C表示点-4i所对应的点,则∠ABC= .
【答案】分析:先求得f (1+ i)=2
i)=2 +2i,可得点B(2
+2i,可得点B(2 ,2).再由点A和点C的坐标,可得
,2).再由点A和点C的坐标,可得 和
和 的坐标、模、以及
的坐标、模、以及  的值,再根据 cos<
的值,再根据 cos< ,
, >=
>= 求得<
求得< ,
, >的值,可得∠ABC的值.
>的值,可得∠ABC的值.
解答:解:∵f(z)=2z(cos +icos
+icos )=2z(
)=2z( -
- i),
i),
∴f (1+ i)=2(1+
i)=2(1+ i)•(
i)•( -
- i)=2
i)=2 +2i,故点B(2
+2i,故点B(2 ,2).
,2).
再由点A(0,0),点C(0,-4),可得 =(-2
=(-2 ,-2),
,-2), =(-2
=(-2 ,-6),
,-6),
∴ =12+12=24,|
=12+12=24,| |=4,|
|=4,| |=4
|=4 ,∴cos<
,∴cos< ,
, >=
>= =
= ,
,
∴< ,
, >=30°,故∠ABC=30°,
>=30°,故∠ABC=30°,
故答案为 30°
点评:本题主要考查复数的代数表示及其几何意义,复数与复平面内对应点之间的关系,两个向量的夹角公式的应用,体现了转化的数学思想,属于基础题.
 i)=2
i)=2 +2i,可得点B(2
+2i,可得点B(2 ,2).再由点A和点C的坐标,可得
,2).再由点A和点C的坐标,可得 和
和 的坐标、模、以及
的坐标、模、以及  的值,再根据 cos<
的值,再根据 cos< ,
, >=
>= 求得<
求得< ,
, >的值,可得∠ABC的值.
>的值,可得∠ABC的值.解答:解:∵f(z)=2z(cos
 +icos
+icos )=2z(
)=2z( -
- i),
i),∴f (1+
 i)=2(1+
i)=2(1+ i)•(
i)•( -
- i)=2
i)=2 +2i,故点B(2
+2i,故点B(2 ,2).
,2).再由点A(0,0),点C(0,-4),可得
 =(-2
=(-2 ,-2),
,-2), =(-2
=(-2 ,-6),
,-6),∴
 =12+12=24,|
=12+12=24,| |=4,|
|=4,| |=4
|=4 ,∴cos<
,∴cos< ,
, >=
>= =
= ,
,∴<
 ,
, >=30°,故∠ABC=30°,
>=30°,故∠ABC=30°,故答案为 30°
点评:本题主要考查复数的代数表示及其几何意义,复数与复平面内对应点之间的关系,两个向量的夹角公式的应用,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目