题目内容
【题目】【扬州市2016—2017学年度第一学期期末检测】（本小题满分14分）
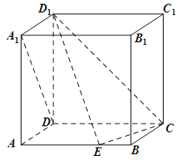
如图，矩形ABCD是一个历史文物展览厅的俯视图，点E在AB上，在梯形BCDE区域内部展示文物，DE是玻璃幕墙，游客只能在
ADE区域内参观．在AE上点P处安装一可旋转的监控摄像头，
为监控角，其中M、N在线段DE（含端点）上，且点M在点N的右下方.经测量得知：AD=6米，AE=6米，AP=2米，
.记
（弧度），监控摄像头的可视区域PMN的面积为S平方米．
（1）求S关于
的函数关系式，并写出的取值范围；（参考数据：
）
（2）求
的最小值.
【答案】见解析
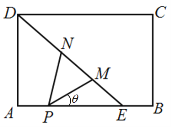
【解析】⑴方法一：在
PME中，
，PE=AE-AP=4米，
，
，
由正弦定理得
，
所以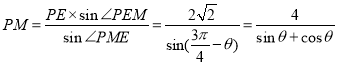
，---------------------2分
同理在PNE中，由正弦定理得
，
所以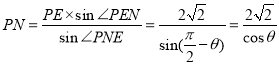
，---------------------4分
所以PMN的面积S
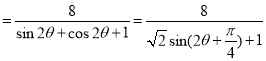，--------------------8分
当M与E重合时，
；当N与D重合时，
,即
，
，
所以
.
综上可得：
,
.---------------------10分
方法二：在PME中，，PE=AE-AP=4米，，，由正弦定理可知：
，
所以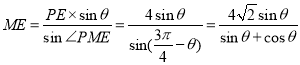
，---------------------2分
在PNE中，由正弦定理可知：
，
所以
，---------------------4分
所以
,
又点P到DE的距离为
，---------------------6分
所以PMN的面积S=
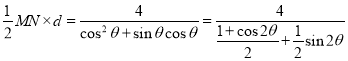
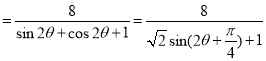，---------------------8分
当M与E重合时，；当N与D重合时，,即，，
所以.
综上可得：,.---------------------10分
⑵当
即
时，
取得最小值为
.---------13分
所以可视区域PMN面积的最小值为
平方米.---------------------14分
阅读快车系列答案
【题目】福州市某大型家电商场为了使每月销售空调和冰箱获得的总利润达到最大，对某月即将出售的空调和冰箱进行了相关调查，得出下表：
资金 | 每台空调或冰箱所需资金（百元） | 月资金最多供应量（百元） | |
空调 | 冰箱 | ||
进货成本 | 30 | 20 | 300 |
工人工资 | 5 | 10 | 110 |
每台利润 | 6 | 8 | |
问：该商场如果根据调查得来的数据，应该怎样确定空调和冰箱的月供应量，才能使商场获得的总利润最大？总利润的最大值为多少元？
