题目内容
判断下列函数是否存在零点,如果存在,请求出.
(1)f(x)=-8x2+7x+1;
(2)f(x)=x2+x+2;
(3)f(x)=
;
(4)f(9x)=3x+1-7;
(5)f(x)=log5(2x-3).
(1)f(x)=-8x2+7x+1;
(2)f(x)=x2+x+2;
(3)f(x)=
| x2+4x-12 | x-2 |
(4)f(9x)=3x+1-7;
(5)f(x)=log5(2x-3).
分析:本题考查函数零点的求法,根据不同的条件使用不同的方法求解.
解答:解:(1)因为f(x)=-8x2+7x+1=-(8x+1)(x-1),令f(x)=0,解得x=-
或x=1,所以函数的零点为-
和1.
(2)令x2+x+2=0,因为△=(-1)2-4×1×2=-7<0,所以方程无实数根,所以f(x)=x2+x+2不存在零点.
(3)因为f(x)=
=
,令
=0,解得x=-6,所以函数的零点为-6.
(4)设t=9x,则x=
,所以f(t)=3
+1-7,即 f(x)=3
+1-7,令f(x)=3
+1-7=0,解得x=9log?3
,所以函数的零点为9log3
.
(5)令log5(2x-3)=0,解得x=2,所以函数的零点为2.
| 1 |
| 8 |
| 1 |
| 8 |
(2)令x2+x+2=0,因为△=(-1)2-4×1×2=-7<0,所以方程无实数根,所以f(x)=x2+x+2不存在零点.
(3)因为f(x)=
| x2+4x-12 |
| x-2 |
| (x+6)(x-2) |
| x-2 |
| (x+6)(x-2) |
| x-2 |
(4)设t=9x,则x=
| t |
| 9 |
| t |
| 9 |
| x |
| 9 |
| x |
| 9 |
| 7 |
| 3 |
| 7 |
| 3 |
(5)令log5(2x-3)=0,解得x=2,所以函数的零点为2.
点评:本题考查函数零点的求法.对应(4)题的零点求法比较难,通过换元可以解决问题.

练习册系列答案
相关题目
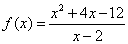 。
。