题目内容
线段AB与CD互相垂直平分于点O,|AB|=2a(a>0),|CD|=2b(b>0).动点P满足|PA|·|PB|=|PC|·|PD|,求P点的轨迹方程.
分析:建立直角坐标系,然后把已知条件用坐标表示,再化简得出所求方程.

解:以O为坐标的点,直线AB、CD分别为x轴、y轴建立直角坐标系,设P(x,y)是所求轨迹上任一点,则A(-a,0),B(a,0),C(0,-b),D(0,b),如图所示.
由|PA|·|PB|=|PC|·|PD|可得
![]() ,化简,得
,化简,得
x2-y2=![]() .
.
点拨:建立直角坐标系是解决此题的关键,建系恰当,可使运算量较小,若建系不当会增加计算量;有时可能得不出正确的结果.

练习册系列答案
相关题目
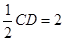 ,点M在线段EC上且不与E、C垂合.
,点M在线段EC上且不与E、C垂合.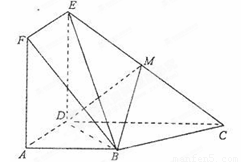
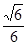 时,求三棱锥M—BDE的体积.
时,求三棱锥M—BDE的体积.