题目内容
如果函数f(x)=ax2+2x-3在区间(-∞,4)上是单调递增的,则实数a的取值范围是( )
A.a>-
| B.a≥-
| C.-
| D.-
|
(1)当a=0时,函数为一次函数f(x)=2x-3为递增函数,
(2)当a>0时,二次函数开口向上,先减后增,在区间(-∞,4)上不可能是单调递增的,故不符合;
(3)当a<0时,函数开口向下,先增后减,函数对称轴-
≥4,
解得a≥-
,又a<0,故-
≤a<0.
综合得-
≤a≤0,
故选D.
(2)当a>0时,二次函数开口向上,先减后增,在区间(-∞,4)上不可能是单调递增的,故不符合;
(3)当a<0时,函数开口向下,先增后减,函数对称轴-
| 1 |
| a |
解得a≥-
| 1 |
| 4 |
| 1 |
| 4 |
综合得-
| 1 |
| 4 |
故选D.

练习册系列答案
相关题目
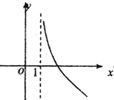
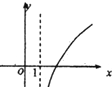
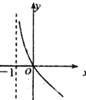

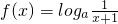 的图象大致是
的图象大致是



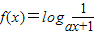 的图象大致是( )
的图象大致是( )



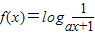 的图象大致是( )
的图象大致是( )



 的图象大致是( )
的图象大致是( )