题目内容
（本小题满分12分）
在数列
中，
．
（1）求证：数列
为等差数列；
（2）设数列
满足
，证明：
对一切
恒成立．
（1）见解析（2）见解析
解析:
（1）
（与
无关） .…………4分
故数列
为等差数列，且公差
. ……………………5分
（2）由（1）可知，
，故
………6分
……………………7分
方法一：数学归纳法
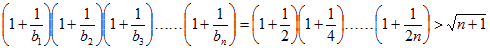
（1）当
时，
，不等式成立， …………8分
（2）假设
时不等式成立，
即
， ………………………….9分
那么当
时，
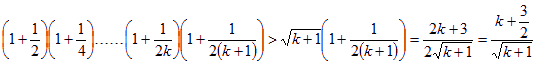
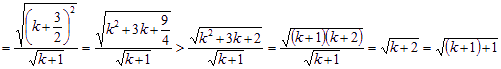
这说明，当时不等式也成立 …………………………………11分
综上可知，对于
，原不等式均成立. ……………………………12分
方法二：均值不等式
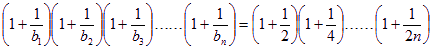
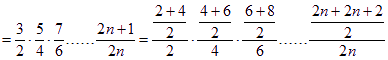……………9分
.
原不等式得证. ……………………12分
练习册系列答案
名校课堂系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
