题目内容
(本小题满分12分)已知椭圆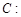
 经过点
经过点 ,一个焦点是
,一个焦点是 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 与
与 轴的两个交点为
轴的两个交点为 、
、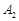 ,点
,点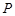 在直线
在直线 上,直线
上,直线 、
、 分别与椭圆
分别与椭圆 交于
交于 、
、 两点.试问:当点
两点.试问:当点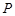 在直线
在直线 上运动时,直线
上运动时,直线 是否恒经过定点
是否恒经过定点 ?证明你的结论.
?证明你的结论.
【答案】
(本小题满分12分)
解:(I)方法1:椭圆的一个焦点是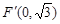 ,
,
∴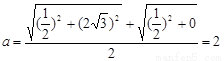 ,
………………(2分)
,
………………(2分)
∵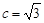 ,∴
,∴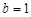 ,∴椭圆方程为
,∴椭圆方程为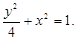 ………………(4分)
………………(4分)
方法2: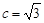 ,可设椭圆方程为
,可设椭圆方程为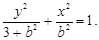 ………………(2分)
………………(2分)
∵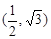 在椭圆上,所以
在椭圆上,所以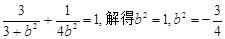 (舍去)
(舍去)
∴椭圆方程为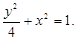 ………………(4分)
………………(4分)
(II)
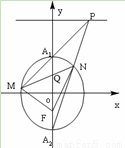
方法1:当点 在
在 轴上时,
轴上时,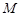 、
、 分别与
分别与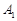 、
、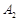 重合,
重合,
若直线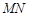 通过定点
通过定点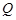 ,则
,则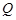 必在
必在 轴上,设
轴上,设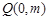 ,………………(6分)
,………………(6分)
当点 不在
不在 轴上时,设
轴上时,设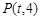 ,
,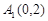 、
、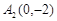 ,
,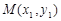 ,
,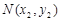
直线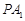 方程
方程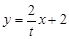 ,
,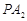 方程
方程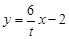 ,
,
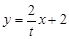 代入
代入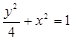 得
得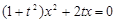 ,
,
解得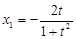 ,
,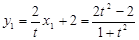 ,
,
∴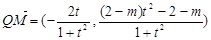 ,
……………(8分)
,
……………(8分)
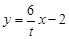 代入
代入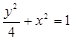 得
得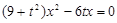
解得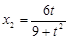 ,
,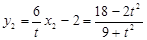 ,
,
∴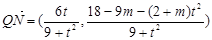 ,
………………(10分)
,
………………(10分)
∵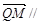
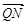 ,
,
∴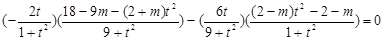 ,
,
∴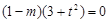 ,
,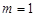 ,
,
∴当点 在直线
在直线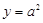 上运动时,直线
上运动时,直线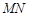 恒经过定点
恒经过定点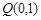 .……………(12分)
.……………(12分)
方法2:直线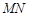 恒经过定点
恒经过定点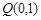 ,证明如下:
,证明如下:
当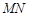 斜率不存在时,直线
斜率不存在时,直线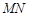 即
即 轴,通过点
轴,通过点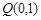 ,……………(6分)
,……………(6分)
当点 不在
不在 轴上时,设
轴上时,设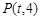 ,
,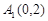 、
、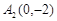 ,
,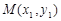 ,
,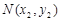
直线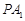 方程
方程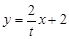 ,
,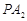 方程
方程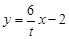 ,
,
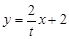 代入
代入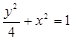 得
得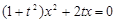 ,
,
得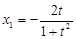 ,
,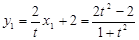 ,∴
,∴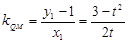 ,……………(8分)
,……………(8分)
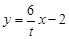 代入
代入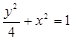 得
得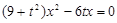
得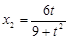 ,
,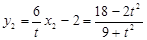 ,
,  …………(10分)
…………(10分)
∴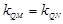 ,直线
,直线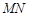 恒经过定点
恒经过定点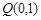 .
………………(12分)
.
………………(12分)
方法3:∵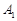 、
、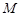 、
、 三点共线,
三点共线, 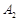 、
、 、
、 三点也共线,
三点也共线,
∴ 是直线
是直线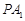 与直线
与直线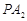 的交点,
的交点,
当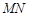 斜率存在时,设
斜率存在时,设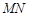 :
: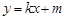 ,代入
,代入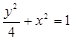 ,
,
得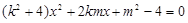 ,
,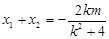 ,
,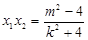 ,
,
直线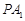 方程
方程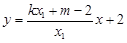 ,直线
,直线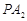 方程
方程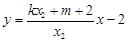 ,
,
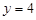 分别代入,得
分别代入,得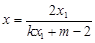 ,
,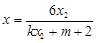 ,
,
∴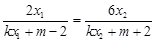 ,即
,即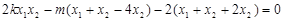 ,
,
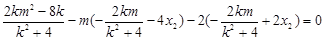 ,
,
∴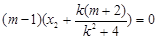 对任意变化的
对任意变化的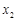 都成立,只能
都成立,只能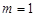 ,
,
∴直线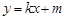 ,通过点
,通过点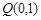
当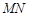 斜率不存在时,直线
斜率不存在时,直线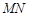 即
即 轴,通过点
轴,通过点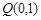 ,……………(10分)
,……………(10分)
∴当点 在直线
在直线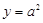 上运动时,直线
上运动时,直线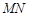 恒经过定点
恒经过定点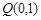 .
.
【解析】略

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目