题目内容
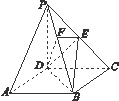
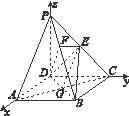
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥BP交BP于点F.
(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD.
 |
证明:以D为坐标原点,射线DA,DC,DP分别为x,y,z轴的正方向建立空间直角坐标系.设DC=2
(1) 连接AC,AC交BD于G,连接EG.依题意得A(2,0,0),P(0,0,2),E(0,1,1).
因为底面ABCD是正方形,所以G是此正方形的中心,故点G的坐标为(1,1,0),
且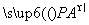 =(2,0,-2),
=(2,0,-2),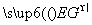 =(1,0,-1).所以
=(1,0,-1).所以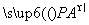 =2
=2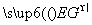 ,这表明PA∥EG.而EG⊂平面EDB且PA⊄平面EDB,所以PA∥平面EDB.
,这表明PA∥EG.而EG⊂平面EDB且PA⊄平面EDB,所以PA∥平面EDB.
(2)依题意得B(2,2,0),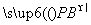 =(2,2,-2).
=(2,2,-2).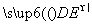 =(0,1,1),故
=(0,1,1),故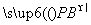 ·
· =0+2-2=0,所以PB⊥DE,由已知EF⊥PB,且EF∩DE=E,所以PB⊥平面EFD.
=0+2-2=0,所以PB⊥DE,由已知EF⊥PB,且EF∩DE=E,所以PB⊥平面EFD.
 |

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 是单位向量,且
是单位向量,且 .若向量
.若向量 满足
满足 ,则
,则 的取值范围是( ).
的取值范围是( ). B.
B.  C.
C.  D.
D. 
 则
则 的最小值是 .
的最小值是 . -
- =1(a>0,b>0)的虚轴长为2,焦距为2
=1(a>0,b>0)的虚轴长为2,焦距为2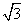 ,则双曲线的渐近线方
,则双曲线的渐近线方 x B.y=±2x C.y=±
x B.y=±2x C.y=± x D.y=±
x D.y=± x
x ”的逆否命题是___________________________.
”的逆否命题是___________________________.



 的定义域是____________.
的定义域是____________. 表示的平面区域为M,若直线y=kx-3k与平面区域M有公共点,则k的取值范围是( ).
表示的平面区域为M,若直线y=kx-3k与平面区域M有公共点,则k的取值范围是( ). B.
B.
 D.
D.