题目内容
若函数f(x)=x2+ax(a∈R),则下列结论正确的是( )
| A.存在a∈R,f(x)是偶函数 |
| B.存在a∈R,f(x)是奇函数 |
| C.对于任意的a∈R,f(x)在(0,+∞)上是增函数 |
| D.对于任意的a∈R,f(x)在(0,+∞)上是减函数 |
A
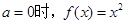 是偶函数;所以A正确;对任意的
是偶函数;所以A正确;对任意的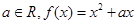 不是奇函数;
不是奇函数;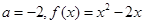 在(0,+∞)上不是增函数,在(1,+∞)上是增函数;
在(0,+∞)上不是增函数,在(1,+∞)上是增函数;因为函数f(x)=x2+ax(a∈R)是开口向上的抛物线,所以对于任意的a∈R,f(x)在(0,+∞)上不是减函数。故选A

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
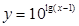 的图象相同的函数是 ( )
的图象相同的函数是 ( )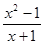
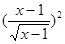
 ) .已知函数y=
) .已知函数y=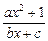 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<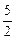
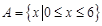 ,
,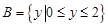 ,从
,从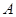 到
到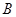 的对应法则
的对应法则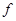 不是映射的是( )
不是映射的是( )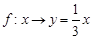 B.
B.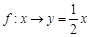 C.
C.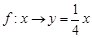 D.
D.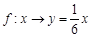
 ,令
,令 ,则函数
,则函数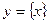 : ①定义域为R; ②值域为
: ①定义域为R; ②值域为 ;③在定义域上是单调增函数; ④是周
;③在定义域上是单调增函数; ④是周 期为1的周期函数; ⑤是奇函数。其中正确判断的序号是_________________(把所有正确的序号都填上)
期为1的周期函数; ⑤是奇函数。其中正确判断的序号是_________________(把所有正确的序号都填上)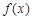 是定义在R上的奇函数,其最小正周期为3, 且
是定义在R上的奇函数,其最小正周期为3, 且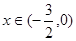 时
时 ,则
,则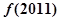 = ( )
= ( )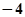
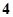
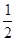
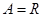 ,
,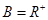 ,f:A→B是从A到B的一个映射,若f:x→2x-1,则B中的元素3的原象为 ( )
,f:A→B是从A到B的一个映射,若f:x→2x-1,则B中的元素3的原象为 ( )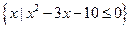 ,B={
,B={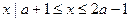 },若B
},若B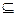 A,则-3
A,则-3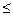 a
a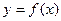 与直线x=l的交点个数为0或l;
与直线x=l的交点个数为0或l;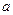
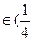 ,+∞)时,函数
,+∞)时,函数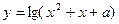
 的值域为R;
的值域为R;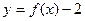 关于点(1,-1)对称的函数为
关于点(1,-1)对称的函数为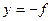 (2 -x
(2 -x ).
).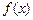 在
在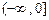 内单调递减,则不等式
内单调递减,则不等式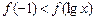 的解集是 .
的解集是 .