Question

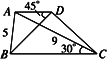
如图所示，在梯形ABCD中，AB=10，CD=6，AD=BC=4，动点P从B点开始沿着折线BC，CD，DA前进至A，若P点运动的路程为x，△PAB的面积为y.

(1)写出y=f(x)的解析式，指出函数的定义域；

(2)画出函数的图像并求出函数的值域.

Answer 1

思路分析：本题考查的是分段函数及函数的定义域、解析式、值域等知识，以及应用知识解决实际问题的能力.首先通过画草图可以发现，P点运动到不同的位置，y的求法是不同的(如图的阴影部分所示).

    可以看出上述三个阴影三角形的底是相同的，它们的面积由其高来定，所以只要由运动路程x来求出各段的高即可.

解：(1)分类讨论：

①当P在BC上运动时，易知∠B=60°，则

y=×10×(xsin60°)=x，0≤x≤4.

②当P点在CD上运动时，

y=×10×4×sin60°=，4＜x≤10.

③当P在DA上运动时，

y=×10×(14-x)sin60°=x+，10＜x≤14.

综上所得，函数的解析式为

y=f(x)=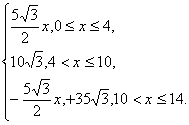

(2)f(x)的图像如图所示.

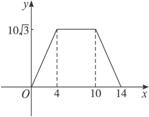
    由图像可知，y的取值范围是0≤y≤，

    即函数f(x)的值域为［0，］.