题目内容
设p:?x∈ 使函数
使函数 有意义,若¬p为假命题,则t的取值范围为 .
有意义,若¬p为假命题,则t的取值范围为 .
【答案】分析:由命题p为真命题,知存在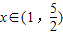 使对数式的真数大于0成立,然后采用分离变量的办法把t分离出来,求出分离变量后的函数的值域,则t的范围可求.
使对数式的真数大于0成立,然后采用分离变量的办法把t分离出来,求出分离变量后的函数的值域,则t的范围可求.
解答:解:若¬P为假命题,则p为真命题.不等式tx2+2x-2>0有属于(1, )的解,即
)的解,即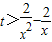 有属于(1,
有属于(1, )的解,
)的解,
又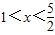 时,
时,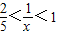 ,所以
,所以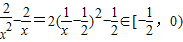 .
.
故t>- .
.
故答案为t>- .
.
点评:本题考查了命题的否定,训练了分离变量法求字母的范围,一个命题与它的否命题真假相反,是中档题.
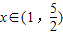 使对数式的真数大于0成立,然后采用分离变量的办法把t分离出来,求出分离变量后的函数的值域,则t的范围可求.
使对数式的真数大于0成立,然后采用分离变量的办法把t分离出来,求出分离变量后的函数的值域,则t的范围可求.解答:解:若¬P为假命题,则p为真命题.不等式tx2+2x-2>0有属于(1,
 )的解,即
)的解,即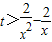 有属于(1,
有属于(1, )的解,
)的解,又
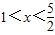 时,
时,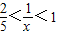 ,所以
,所以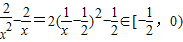 .
.故t>-
 .
.故答案为t>-
 .
.点评:本题考查了命题的否定,训练了分离变量法求字母的范围,一个命题与它的否命题真假相反,是中档题.

练习册系列答案
相关题目
 使函数
使函数 有意义,若¬p为假命题,则t的取值范围为 .
有意义,若¬p为假命题,则t的取值范围为 .