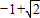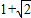题目内容
连接抛物线x2=4y的焦点F与点M(1,0)所得的线段与抛物线交于点A,设点O为坐标原点,则△OAM的面积为 .
【答案】分析:设线段FM所在直线方程x+y=1与抛物线交于A(x,y),与抛物线方程联立求得y,进而根据三角形面积公式求得答案.
解答:解:线段FM所在直线方程x+y=1与抛物线交于A(x,y),
则
∴y=3-2 或y=3+2
或y=3+2 (舍去).
(舍去).
∴S△OAM= ×1×(3-2
×1×(3-2 )=
)= .
.
故答案为 .
.
点评:本题主要考查了抛物线的应用.考查了学生对直线与圆锥曲线关系知识的理解和应用.
解答:解:线段FM所在直线方程x+y=1与抛物线交于A(x,y),
则

∴y=3-2
 或y=3+2
或y=3+2 (舍去).
(舍去).∴S△OAM=
 ×1×(3-2
×1×(3-2 )=
)= .
.故答案为
 .
.点评:本题主要考查了抛物线的应用.考查了学生对直线与圆锥曲线关系知识的理解和应用.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
连接抛物线x2=4y的焦点F与点M(1,0)所得的线段与抛物线交于点A,设点O为坐标原点,则三角形OAM的面积为( )
A、-1+
| ||||
B、
| ||||
C、1+
| ||||
D、
|