题目内容
(2014•广东模拟)已知数列{an}的前n项和是Sn,且Sn+
an=1(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=log3(1-Sn+1)(n∈N*),求适合方程
+
+…+
=
的正整数n的值.
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)设bn=log3(1-Sn+1)(n∈N*),求适合方程
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
| 25 |
| 51 |
分析:(1)由S n+
an=1,得Sn-1+
an-1=1(n≥2),两式相减得an与an-1的递推式,由递推式易判断数列{an}为等比数列,从而可求an;
(2)由(1)易求得1-Sn+1,进而可求bn,利用裂项相消法可求得
+
+…+
,从而可把方程变为关于n的方程,解出即可;
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)易求得1-Sn+1,进而可求bn,利用裂项相消法可求得
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
解答:解:(1)由S n+
an=1,得Sn-1+
an-1=1(n≥2),
两式相减得,an+
an-
an-1=0(n≥2),即an=
an-1(n≥2),
由S n+
an=1得S1+
a1=1,即
a1=1,解得a1=
,
所以数列{an}各项均不为0,且是以
为首项、
为公比的等比数列,
所以an=
×(
)n-1=
;
(2)由(1)知,Sn+1+
an+1=1,即1-Sn+1=
an+1=
,
所以b n=lo
=log3
=-(n+1),
则
=
=
-
,
所以
+
+…+
=
-
+
-
+…+
-
=
-
,
所以方程
+
+…+
=
即
-
=
,解得n=100,
故适合方程
+
+…+
=
的正整数n的值为100.
| 1 |
| 2 |
| 1 |
| 2 |
两式相减得,an+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
由S n+
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
所以数列{an}各项均不为0,且是以
| 2 |
| 3 |
| 1 |
| 3 |
所以an=
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3n |
(2)由(1)知,Sn+1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3n+1 |
所以b n=lo
| g | (1-Sn+1) 3 |
| 1 |
| 3n+1 |
则
| 1 |
| bnbn+1 |
| 1 |
| -(n+1)[-(n+2)] |
| 1 |
| n+1 |
| 1 |
| n+2 |
所以
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| n+2 |
所以方程
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
| 25 |
| 51 |
| 1 |
| 2 |
| 1 |
| n+2 |
| 25 |
| 51 |
故适合方程
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
| 25 |
| 51 |
点评:本题考查由数列递推公式求通项公式,考查等比数列及用列项相消法进行数列求和,熟练掌握an与Sn间的关系是解决本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
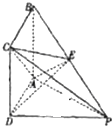 (2014•广东模拟)如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP.
(2014•广东模拟)如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP.