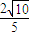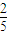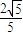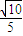题目内容
已知直线和参数方程为
,是椭圆
上任意一点，求点到直线的距离的最大值．
解析:
直线的参数方程为为参数）故直线的普通方程为
3分
因为为椭圆上任意点，故可设
其中
.
因此点到直线的距离是 7分
所以当
，时，取得最大值. 10分
练习册系列答案
相关题目
已知直线和参数方程为
（t为参数），P是椭圆
+y2=1上任意一点，则点P到直线的距离的最大值为（ ）
|
| x2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
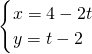（t为参数），P是椭圆
上任意一点，则点P到直线的距离的最大值为
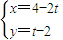（t为参数），P是椭圆
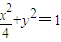上任意一点，则点P到直线的距离的最大值为（ ）
