Question

（本小题满分12分）已知函数.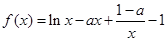

(Ⅰ)当时，讨论的单调性；

（Ⅱ）当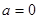时，对于任意的，证明：不等式

 

Answer 1

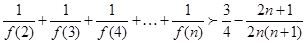
【答案】

（I）原函数的定义域为，因为

当时，所以此时函数上是增函数，在上是减函数；

当时，令，解得（舍去），此时函数在上增函数，在上是减函数；根据的单调性，变形得得

，令证得。

当时，令，解得

此时函数在上是增函数，在和上是减函数   ………6分

（II）由（I）知：时，上是增函数，

设

则

恒成立    单调递减

又

不等式得证                              …………………………………12分

【解析】(Ⅰ)求导函数，讨论a对单调性的影响；