题目内容
曲线f(x)=(x-3)ex,当x∈(2,+∞)时,f(x)>k恒成立,则实数k的取值范围是________.
(-∞,-e2]
分析:x∈(2,+∞)时,f(x)>k恒成立,等价于f(x)min>k,利用导数判断f(x)的单调性,由单调性即可求得其最小值.
解答:f′(x)=ex+(x-3)ex=ex(x-2),
当x∈(2,+∞)时,f′(x)>0,
所以f(x)在(2,+∞)上单调递增,f(x)>f(2)=-e2,
因为x∈(2,+∞)时,f(x)>k恒成立,
所以-e2≥k,即实数k的取值范围是(-∞,-e2].
故答案为:(-∞,-e2].
点评:本题考查利用导数研究函数的最值,考查函数恒成立问题,函数恒成立往往转化为函数最值解决,本题需要注意k与最小值的关系,含有等号.
分析:x∈(2,+∞)时,f(x)>k恒成立,等价于f(x)min>k,利用导数判断f(x)的单调性,由单调性即可求得其最小值.
解答:f′(x)=ex+(x-3)ex=ex(x-2),
当x∈(2,+∞)时,f′(x)>0,
所以f(x)在(2,+∞)上单调递增,f(x)>f(2)=-e2,
因为x∈(2,+∞)时,f(x)>k恒成立,
所以-e2≥k,即实数k的取值范围是(-∞,-e2].
故答案为:(-∞,-e2].
点评:本题考查利用导数研究函数的最值,考查函数恒成立问题,函数恒成立往往转化为函数最值解决,本题需要注意k与最小值的关系,含有等号.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
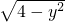 ,存在自公切线的是
,存在自公切线的是 ,存在自公切线的是( )
,存在自公切线的是( ) ,存在自公切线的是( )
,存在自公切线的是( )