题目内容
已知数列{an}满足: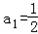 ,2an+1=anan+1+1
,2an+1=anan+1+1
(Ⅰ)求a2,a3,a4;
(Ⅱ)猜想数列{an}的通项公式,并证明你的结论;
(Ⅲ)已知数列{bn}满足:anbn=1﹣an,Sn为数列{bn}的前n项和,证明:S1+S2+…+Sn﹣1=n(Sn﹣1)
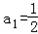 ,2an+1=anan+1+1
,2an+1=anan+1+1(Ⅰ)求a2,a3,a4;
(Ⅱ)猜想数列{an}的通项公式,并证明你的结论;
(Ⅲ)已知数列{bn}满足:anbn=1﹣an,Sn为数列{bn}的前n项和,证明:S1+S2+…+Sn﹣1=n(Sn﹣1)
(Ⅰ)解:∵数列{an}满足: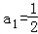 ,2an+1=anan+1+1
,2an+1=anan+1+1
∴n=1时,2a2=a1a2+1,∴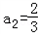
n=2时,2a3=a2a3+1,∴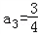
n=3时,2a4=a3a4+1,∴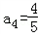 ;
;
(Ⅱ)猜想数列{an}的通项公式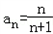 ,
,
证明:①当n=1,2,3,4时,由(Ⅰ)知结论成立;
②假设n=k时,结论成立,即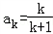 ,则n=k+1时,∴2an+1=anan+1+1
,则n=k+1时,∴2an+1=anan+1+1
∴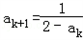 =
=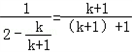
即n=k+1时,结论成立
由①②可知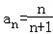 ;
;
(Ⅲ)解:由anbn=1﹣an,可得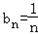
∴S1+S2+…+Sn﹣1=(n﹣1)+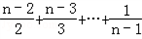
=n+
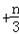 +…+
+…+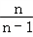 ﹣1×(n﹣1)
﹣1×(n﹣1)
=n(1+ +…+
+…+ ﹣1)
﹣1)
=n(Sn﹣1)
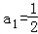 ,2an+1=anan+1+1
,2an+1=anan+1+1∴n=1时,2a2=a1a2+1,∴
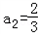
n=2时,2a3=a2a3+1,∴
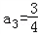
n=3时,2a4=a3a4+1,∴
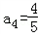 ;
;(Ⅱ)猜想数列{an}的通项公式
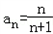 ,
,证明:①当n=1,2,3,4时,由(Ⅰ)知结论成立;
②假设n=k时,结论成立,即
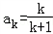 ,则n=k+1时,∴2an+1=anan+1+1
,则n=k+1时,∴2an+1=anan+1+1∴
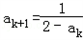 =
=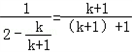
即n=k+1时,结论成立
由①②可知
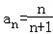 ;
;(Ⅲ)解:由anbn=1﹣an,可得
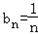
∴S1+S2+…+Sn﹣1=(n﹣1)+
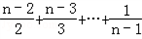
=n+

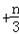 +…+
+…+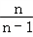 ﹣1×(n﹣1)
﹣1×(n﹣1)=n(1+
 +…+
+…+ ﹣1)
﹣1)=n(Sn﹣1)

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目