题目内容
在平面直角坐标系xOy中,以O为极点,Ox为极轴建立极坐标系,且两种坐标系长度单位一致.已知直线l的极坐标方程为ρcos(θ+ )=
)= -1,圆C在直角坐标系中的参数方程为
-1,圆C在直角坐标系中的参数方程为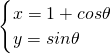 (θ为参数),求直线l与圆C的公共点的个数.
(θ为参数),求直线l与圆C的公共点的个数.
解:将方程ρcos(θ+ )=
)= -1化为直角坐标方程:x-y+
-1化为直角坐标方程:x-y+ -1=0.
-1=0.
将参数方程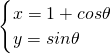 化为普通方程:(x-1)2+y2=1.
化为普通方程:(x-1)2+y2=1.
圆心(1,0)到直线l的距离d= =1,而圆C的半径为1,
=1,而圆C的半径为1,
所以直线l与圆C相切,即它们的公共点的个数为1.
分析:把极坐标方程化为直角坐标方程,把参数方程化为普通方程,求出圆心(1,0)到直线l的距离,与半径作对照,即得直线l与圆C的公共点的个数.
点评:本题考查参数方程与普通方程之间的转化,把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,求出圆心(1,0)到直线l的距离,是解题的关键.
 )=
)= -1化为直角坐标方程:x-y+
-1化为直角坐标方程:x-y+ -1=0.
-1=0.将参数方程
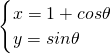 化为普通方程:(x-1)2+y2=1.
化为普通方程:(x-1)2+y2=1.圆心(1,0)到直线l的距离d=
 =1,而圆C的半径为1,
=1,而圆C的半径为1,所以直线l与圆C相切,即它们的公共点的个数为1.
分析:把极坐标方程化为直角坐标方程,把参数方程化为普通方程,求出圆心(1,0)到直线l的距离,与半径作对照,即得直线l与圆C的公共点的个数.
点评:本题考查参数方程与普通方程之间的转化,把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,求出圆心(1,0)到直线l的距离,是解题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,一条渐近线方程为x-2y=0,则它的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.