题目内容
设M为部分正整数组成的集合，数列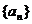
的首项
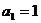，前n项和为
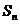，已知对任意整数k属于M，当n>k时，
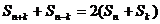都成立。
（1）设M=｛1｝，
，求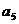
的值；（2）设M=｛3，4｝，求数列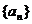的通项公式。
【答案】
解析：（1）
即：
所以，n>1时，
成等差，而
，
（2）由题意：
，
当
时，由（1）（2）得：
由（3）（4）得： 
由（1）（3）得：
由（2）（4）得：
由（7）（8）知：
成等差，
成等差；设公差分别为：
由（5）（6）得：
由（9）（10）得：
成等差，设公差为d,
在（1）（2）中分别取n=4,n=5得：
练习册系列答案
相关题目
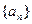的首项
，前n项和为
，已知对任意整数k属于M，当n>k时，
都成立。
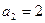，求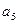
的值；（2）设M=｛3，4｝，求数列