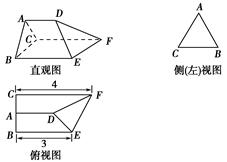
题目内容
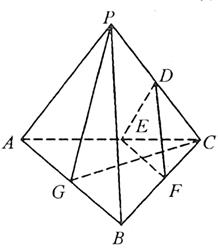
如图,在三棱锥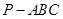 中,
中,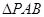 和
和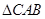 都是以
都是以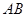 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,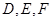 分别是
分别是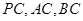 的中点.
的中点.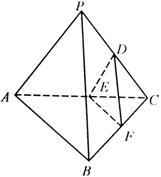
(1)证明:平面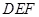 //平面
//平面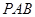 ;
;
(2)证明: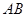
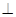
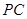 ;
;
(3)若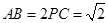 ,求三棱锥
,求三棱锥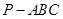 的体积.
的体积.
(1)证明过程详见试题解析;(2)证明过程详见试题解析;(3)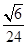 .
.
解析试题分析:(1)要证明平面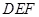 //平面
//平面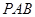 ,就是要在一个平面内找两条相交直线平行另一个平面,从题目所给出的条件可以容易得到在平面
,就是要在一个平面内找两条相交直线平行另一个平面,从题目所给出的条件可以容易得到在平面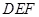 中,
中,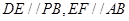 ,从而得到平面
,从而得到平面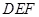 //平面
//平面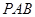 ;(2)要证明
;(2)要证明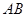
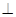
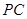 ,可取
,可取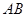 的中点
的中点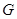 ,连结
,连结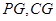 ,由条件得到
,由条件得到 ,由于
,由于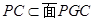 ,所以有
,所以有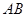
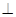
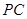 ;(3)由于
;(3)由于 ,所以求三棱锥
,所以求三棱锥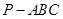 的体积可以转化成求
的体积可以转化成求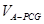 和
和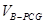 ,而
,而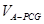 和
和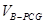 即可整合成
即可整合成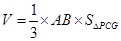 ,所以求得
,所以求得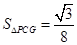 ,可得所求体积为
,可得所求体积为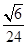 .
.
试题解析:(1)证明:∵ E、F分别是AC、BC的中点,
∴ 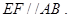
∵ 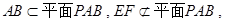
∴ 
∵ 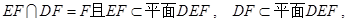
∴ 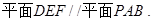
(2)证明:取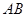 的中点
的中点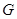 ,连结
,连结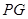 、
、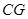 ,
,
∵ △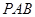 和△
和△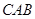 都是以
都是以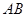 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,
∴ 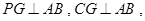
∵ 
∴ 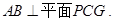
∵ 
∴ 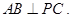
(3)解:在等腰直角三角形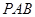 中,
中,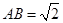 ,
,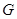 是斜边
是斜边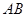 的中点,
的中点,
∴ 
同理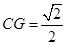 .
.
∵ 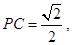
∴ △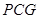 是等边三角形,
是等边三角形,
∴ 
∵ 
所以 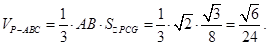
考点:线面平行;面面平行;线线垂直;线面垂直;棱锥的体积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,底面
,底面 是等腰梯形,且
是等腰梯形,且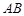 ∥
∥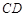 ,
, 是
是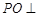 平面
平面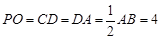 ,
, 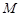 是
是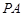 中点.
中点.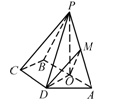
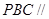 平面
平面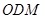 ;(2)求点
;(2)求点 到平面
到平面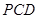 的距离.
的距离. A1B1C1中,∠BAC=90°,AB=AC=
A1B1C1中,∠BAC=90°,AB=AC=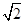 ,AA1=3,D是BC的中点,点E在棱BB1上运动.
,AA1=3,D是BC的中点,点E在棱BB1上运动.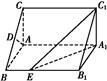
 A1B1E的体积.
A1B1E的体积. 为圆
为圆 的直径,点
的直径,点 .
.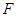 在圆
在圆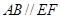 ,矩形
,矩形 所在的平面和圆
所在的平面和圆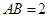 ,
,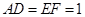 .
.
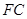 的中点为
的中点为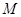 ,求证:
,求证: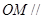 平面
平面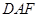 ;
;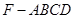 的体积.
的体积.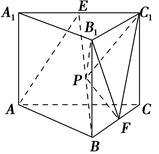
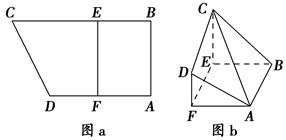
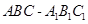 中,
中,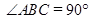 ,
,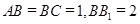 ,求:
,求: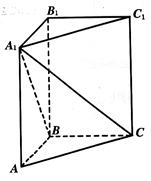
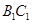 与
与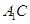 所成角的大小;
所成角的大小; 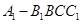 的体积.
的体积.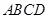 的对角线交于点G,AD⊥平面
的对角线交于点G,AD⊥平面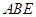 ,
, ,
, ,
,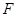 为
为 上的点,且BF⊥平面ACE
上的点,且BF⊥平面ACE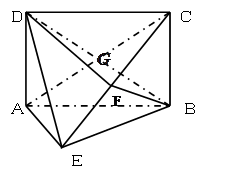
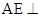 平面
平面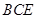 ;
;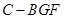 的体积.
的体积.