题目内容
已知函数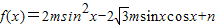 ,(m>0)的定义域为
,(m>0)的定义域为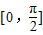 ,值域为[-5,4].
,值域为[-5,4].(1)求m、n的值;
(2)若将函数y=f(x),x∈R的图象按向量
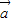 平移后关于原点中心对称,求向量
平移后关于原点中心对称,求向量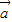 的坐标.
的坐标.
【答案】分析:(1)先利用辅助角公式进行化简整理,然后讨论m的正负,根据x的范围建立方程组,从而可求出所求;
(2)根据(1)分别求出函数的对称中心,从而可求出向量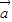 的坐标.
的坐标.
解答:解:(1)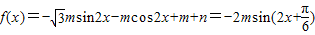 +m+n,
+m+n,
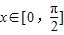
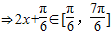
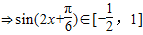 ,(4分)
,(4分)
1°若m>0,则f(x)max=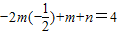 ,f(x)min=-m+n=-5
,f(x)min=-m+n=-5
解得m=3,n=-2,(6分)
2°若m<0,则f(x)max=-m+n=4,f(x)min=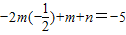
解得m=-3,n=1,(8分)
(2)令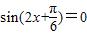 ,解得
,解得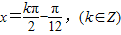 ,(10分)
,(10分)
1°当m=3,n=-2时,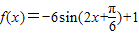 ,
,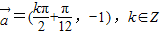 (12分)
(12分)
2°当m=-3,n=1时,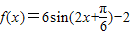 ,
,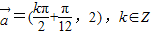 (14分)
(14分)
点评:本题主要考查了三角函数中的恒等变换应用,以及平面向量坐标表示的应用,同时考查了分类讨论的数学思想和计算能力,属于中档题.
(2)根据(1)分别求出函数的对称中心,从而可求出向量
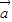 的坐标.
的坐标.解答:解:(1)
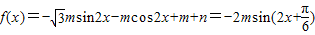 +m+n,
+m+n,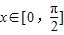
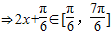
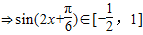 ,(4分)
,(4分)1°若m>0,则f(x)max=
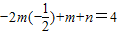 ,f(x)min=-m+n=-5
,f(x)min=-m+n=-5解得m=3,n=-2,(6分)
2°若m<0,则f(x)max=-m+n=4,f(x)min=
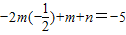
解得m=-3,n=1,(8分)
(2)令
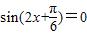 ,解得
,解得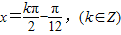 ,(10分)
,(10分)1°当m=3,n=-2时,
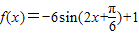 ,
,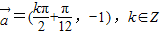 (12分)
(12分)2°当m=-3,n=1时,
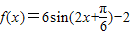 ,
,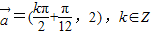 (14分)
(14分)点评:本题主要考查了三角函数中的恒等变换应用,以及平面向量坐标表示的应用,同时考查了分类讨论的数学思想和计算能力,属于中档题.

练习册系列答案
相关题目
 ,其中m>0.
,其中m>0.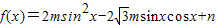 ,(m>0)的定义域为
,(m>0)的定义域为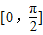 ,值域为[-5,4].
,值域为[-5,4].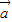 平移后关于原点中心对称,求向量
平移后关于原点中心对称,求向量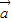 的坐标.
的坐标.