Question

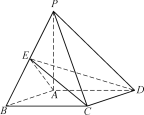
【题目】如图，在三棱锥中，，侧面底面，，为线段上一点，且满足.

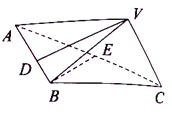
（1）若为的中点，求证：；

（2）当最小时，求二面角的余弦值.

Answer 1

【答案】(1)见证明；(2)

【解析】

(1)根据中点可得 ，再根据面面垂直的性质定理得面，即可证明结论(2) 以为坐标原点，分别以射线和垂直于面向上的方向为轴，建立空间直角坐标系，求出两个半平面的法向量，利用公式求其夹角余弦即可.

（1）在，因为,，

为的中点，所以，

因为面面，面面，所以面，

又面，

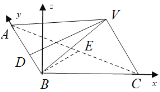
（2）以为坐标原点，分别以射线和垂直于面向上的方向为轴，建立空间直角坐标系，

设，则有，因为侧面底面，，

所以，

所以，

当时，最小，

此时，，

设为平面的一个法向量，则有，

所以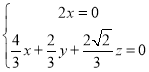，令，则，

而平面的一个法向量为，

所以，

故二面角的余弦值为.