题目内容
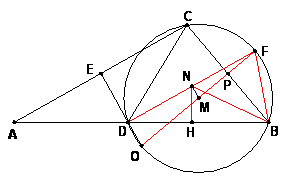
 如图,
如图,![]() 的外心为
的外心为![]() ,
,![]() 是
是![]() 的中点,直线
的中点,直线![]() 交
交![]() 于
于![]() ,点
,点![]() 分别是
分别是![]() 的外心与内心,若
的外心与内心,若![]() ,
,
证明:![]() 为直角三角形.
为直角三角形.
证:由于点![]() 皆在
皆在![]() 的中垂线上,设直线
的中垂线上,设直线![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,则
,则![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点; 因
的中点; 因![]() 是
是![]() 的内心,故
的内心,故![]() 共线,且
共线,且![]() .
.
 又
又 ![]() 是
是![]() 的中垂线,则
的中垂线,则![]() ,而
,而![]() 为
为![]() 的内、外角平分线,故有
的内、外角平分线,故有![]() ,则
,则![]() 为
为![]() 的直径,所以,
的直径,所以,![]() ,又因
,又因
![]()
![]() ,
,
则![]() . 作
. 作![]() 于
于![]() ,则有,
,则有,
![]()
![]()
![]() ,且
,且![]() ,所以,
,所以,![]() ,故得
,故得 ![]() ,因此,
,因此,![]() 是
是![]() 的中位线,从而
的中位线,从而 ![]() ∥
∥![]() ,而
,而![]() ,则
,则![]() .故
.故![]() 为直角三角形.
为直角三角形.
证二:记![]() ,因
,因![]() 是
是![]() 的中垂线,则
的中垂线,则![]() ,由条件
,由条件![]() 1
1
延长![]() 交
交![]() 于
于![]() ,并记
,并记![]() ,则
,则![]() ,对圆内接四边形
,对圆内接四边形![]() 用托勒密定理得
用托勒密定理得![]() ,即
,即![]() 2,由1、2得
2,由1、2得![]() ,所以
,所以![]() ,
,
即![]() 是弦
是弦![]() 的中点,而
的中点,而![]() 为外心,所以
为外心,所以![]() ,故
,故![]() 为直角三角形.
为直角三角形.

练习册系列答案
相关题目