题目内容
利用函数的单调性求函数y=x+
的值域．
解：∵函数y=x与函数y=在其定义域[-
，+∞）上均为增函数
由函数单调性的性质得：
函数y=x+在区间[-，+∞）为增函数
故当x=-时，函数取最小值-
故函数的值域为[-，+∞）
分析：由函数的单调性的性质，结合函数y=x与函数y=的单调性，我们易判断函数y=x+在区间[-，+∞）的单调性，进而求出函数y=x+的值域．
点评：本题考查的知识点是函数的单调性的性质，其中根据函数的单调性的性质，判断函数y=x+在区间[-，+∞）的单调性是解答本题的关键．
在其定义域[-，+∞）上均为增函数 由函数单调性的性质得：
函数y=x+
在区间[-，+∞）为增函数故当x=-
时，函数取最小值-故函数的值域为[-
，+∞）分析：由函数的单调性的性质，结合函数y=x与函数y=
的单调性，我们易判断函数y=x+在区间[-，+∞）的单调性，进而求出函数y=x+的值域．点评：本题考查的知识点是函数的单调性的性质，其中根据函数的单调性的性质，判断函数y=x+
在区间[-，+∞）的单调性是解答本题的关键． 
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
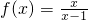，x∈[2，4]是单调递减函数，并求函数的值域．
，x∈[2，4]是单调递减函数，并求函数的值域．