题目内容
已知数列an的通项公式an=
(n∈N+),记f(n)=(1-a1)(1-a2)…(1-an),试通过计算f(1),f(2),f(3)的值,推测出f(n)的值.
| 1 |
| (n+1)2 |
∵f(n)=(1-a1)(1-a2)…(1-an),
f(1)=1-a1=1-
=
,(2分)
f(2)=(1-a1)(1-a2)=f(1)•(1-
)=
•
=
=
,(4分)f(3)=(1-a1)(1-a2)(1-a3)=f(2)•(1-
)=
•
=
.(6分)
根据其结构特点可得:f(n)=
.(12分)
f(1)=1-a1=1-
| 1 |
| 4 |
| 3 |
| 4 |
f(2)=(1-a1)(1-a2)=f(1)•(1-
| 1 |
| 9 |
| 3 |
| 4 |
| 8 |
| 9 |
| 2 |
| 3 |
| 4 |
| 6 |
| 1 |
| 16 |
| 2 |
| 3 |
| 15 |
| 16 |
| 5 |
| 8 |
根据其结构特点可得:f(n)=
| n+2 |
| 2(n+1) |

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目

 ;
; ,求
,求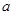 的取值范围.
的取值范围. 的解集是 .
的解集是 . ,解关于
,解关于 的不等式
的不等式
 ,
, ,它的最小项是 。
,它的最小项是 。