题目内容
(本小题满分12分)
已知点![]() 是椭圆
是椭圆![]() 的右焦点,点
的右焦点,点![]() 、
、![]() 分别是
分别是![]() 轴、
轴、![]() 轴上的动点,且满足
轴上的动点,且满足![]() .若点
.若点![]() 满足
满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设过点![]() 任作一直线与点
任作一直线与点![]() 的轨迹交于
的轨迹交于![]() 、
、![]() 两点,直线
两点,直线![]() 、
、![]() 与直线
与直线![]() 分别交于点
分别交于点![]() 、
、![]() (
(![]() 为坐标原点),试判断
为坐标原点),试判断![]() 是否为定值?若是,求出这个定值;若不是,请说明理由.
是否为定值?若是,求出这个定值;若不是,请说明理由.
解:(Ⅰ) ![]() 椭圆
椭圆![]() 右焦点
右焦点![]() 的坐标为
的坐标为![]() , ………(1分)
, ………(1分)
![]() .
.![]() ,
,
![]() 由
由![]() ,得
,得![]() . ………… (2分)
. ………… (2分)
设点![]() 的坐标为
的坐标为![]() ,由
,由![]() ,有
,有![]() ,
,
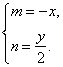 代入
代入![]() ,得
,得![]() . ……… (4分)
. ……… (4分)
(Ⅱ)解法一:设直线![]() 的方程为
的方程为![]() ,
,![]() 、
、![]() ,
,
则![]() ,
,![]() . ………… (5分)
. ………… (5分)
由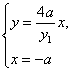 ,得
,得![]() , 同理得
, 同理得![]() . ………… (7分)
. ………… (7分)
![]() ,
,![]() ,则
,则![]() . ……(8分)
. ……(8分)
由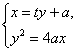 ,得
,得![]() ,
,![]() . ……… (9分)
. ……… (9分)
则![]() . …………… (11分)
. …………… (11分)
因此,![]() 的值是定值,且定值为
的值是定值,且定值为![]() . ……… (12分)
. ……… (12分)
解法二:①当![]() 时,
时, ![]() 、
、![]() ,则
,则![]() ,
, ![]() .
.
由![]() 得点
得点![]() 的坐标为
的坐标为![]() ,则
,则![]() .
.
由![]() 得点
得点![]() 的坐标为
的坐标为![]() ,则
,则![]() .
.
![]()
![]() . …………… (6分)
. …………… (6分)
②当![]() 不垂直
不垂直![]() 轴时,设直线
轴时,设直线![]() 的方程为
的方程为![]() ,
,![]() 、
、![]() ,同解法一,得
,同解法一,得![]() . … (8分)
. … (8分)
由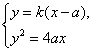 ,得
,得![]() ,
,![]() . …………(9分)
. …………(9分)
则![]() . ………… (11分)
. ………… (11分)
因此,![]() 的值是定值,且定值为
的值是定值,且定值为![]() . ………… (12分)
. ………… (12分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目