题目内容
 如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )分析:利用三角形全等即可得出△ADE及△AB′E的面积,进而可求出阴影部分的面积.
解答:解:如图所示,假设CD与C′B′相较于点E.连接AE.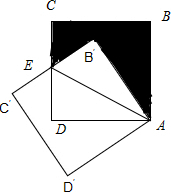
∵AD=AB′,AE边公用,∴Rt△ADE≌Rt△AB′E.
∴∠B′AE=∠DAE=∠DAD′=30°.
∴DE=1×tan30°=
.
∴S△ADE=
×
×1=
=S△AB′E.
∴图中阴影部分的面积S=12-2×
=1-
.
故选A.

∵AD=AB′,AE边公用,∴Rt△ADE≌Rt△AB′E.
∴∠B′AE=∠DAE=∠DAD′=30°.
∴DE=1×tan30°=
| ||
| 3 |
∴S△ADE=
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
∴图中阴影部分的面积S=12-2×
| ||
| 6 |
| ||
| 3 |
故选A.
点评:熟练掌握三角形全等的判定方法和正方形的性质是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
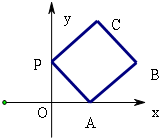 (北京卷理14)如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为
(北京卷理14)如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为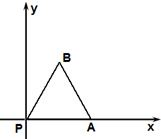 如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是
如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是 如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),设f(x)的最小正周期为T,y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为S,则ST=
如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),设f(x)的最小正周期为T,y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为S,则ST= (2011•洛阳一模)如图放置的边长为1的正三角形ABC沿x轴的正方向滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系是y=f(x).则f(x)在两个相邻零点间的图象与x轴围成的面积是
(2011•洛阳一模)如图放置的边长为1的正三角形ABC沿x轴的正方向滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系是y=f(x).则f(x)在两个相邻零点间的图象与x轴围成的面积是