Question

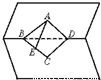
如下图，∠BAD=90°的等腰Rt△ABD与正△CBD所在平面成60°的二面角，则AB与平面BCD所成角的大小为_____________.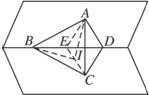

Answer 1

arcsin

解析：取BD的中点E，连结AE、CE、AC.

∵AB=AD，BC=CD，

∴∠AEC为二面角BCD-ABD的平面角，为60°.

作AF⊥CE于F，连结BF，则∠ABF为AB与面BCD所成的角.

设AD=AB=a，则AE=a.

AF=AE·sin60°=a.

∴sinABF==,

即∠ABF=arcsin.