题目内容
请您设计一个帐篷,它下部的形状是高为1 m的正六棱柱,上部的形状是侧棱长为3 m的正六棱锥(如右图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大?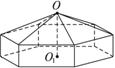
解:设OO1为x m,则1<x<4.由题设可得正六棱锥底面边长为(单位:m)
![]() =
=![]() .于是底面正六边形的面积为(单位:m2)
.于是底面正六边形的面积为(单位:m2)
6·![]() ·(
·(![]() )2=
)2=![]() (8+2x-x2).
(8+2x-x2).
帐篷的体积为(单位:m3)V(x)=![]() (8+2x-x2)[
(8+2x-x2)[![]() (x-1)+1]=
(x-1)+1]=![]() (16+12x-x3).
(16+12x-x3).
求导数,得V′(x)=![]() (12-3x2).
(12-3x2).
令V′(x)=0,解得x=-2(不合题意,舍去),x=2.当1<x<2时,V′(x)>0,V(x)为增函数;
当2<x<4时,V′(x)<0,V(x)为减函数.所以当x=2时,V(x)最大.答:当OO1为2 m时,帐篷的体积最大.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
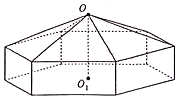 请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大?
请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大?
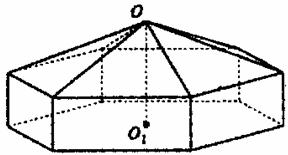
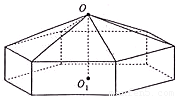 请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心o1的距离为多少时,帐篷的体积最大?
请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心o1的距离为多少时,帐篷的体积最大?