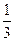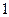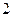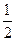题目内容
(本小题满分13分)如图,由不大于n(n∈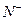 )的正有理数排成的数表,质点按
)的正有理数排成的数表,质点按
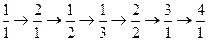
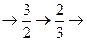 ……顺序跳动,
……顺序跳动,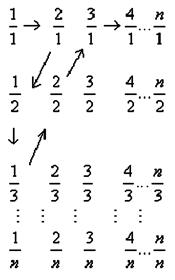
所经过的有理数依次排列构成数列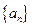 。
。
(Ⅰ)质点从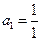 出发,通过抛掷骰子来决定质点的跳动步数,骰子的点数为奇数时,质点往前跳一步(从
出发,通过抛掷骰子来决定质点的跳动步数,骰子的点数为奇数时,质点往前跳一步(从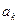 到达
到达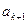 );骰子的点数为偶数时,质点往前跳二步(从
);骰子的点数为偶数时,质点往前跳二步(从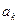 到达
到达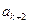 ).
).
①抛掷骰子二次,质点到达的有理数记为ξ,求Eξ;②求质点恰好到达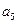 的概率。
的概率。
(Ⅱ)试给出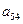 的值(不必写出求解过程)。
的值(不必写出求解过程)。
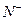 )的正有理数排成的数表,质点按
)的正有理数排成的数表,质点按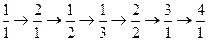
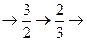 ……顺序跳动,
……顺序跳动,
所经过的有理数依次排列构成数列
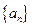 。
。(Ⅰ)质点从
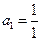 出发,通过抛掷骰子来决定质点的跳动步数,骰子的点数为奇数时,质点往前跳一步(从
出发,通过抛掷骰子来决定质点的跳动步数,骰子的点数为奇数时,质点往前跳一步(从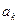 到达
到达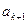 );骰子的点数为偶数时,质点往前跳二步(从
);骰子的点数为偶数时,质点往前跳二步(从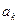 到达
到达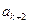 ).
).①抛掷骰子二次,质点到达的有理数记为ξ,求Eξ;②求质点恰好到达
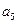 的概率。
的概率。(Ⅱ)试给出
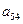 的值(不必写出求解过程)。
的值(不必写出求解过程)。(Ⅰ)①ξ的分布列为
Eξ=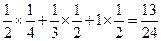
②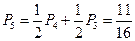
(Ⅱ)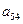 =
=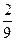
| ξ | 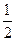 | 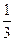 | 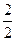 |
| P | 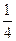 | 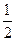 | 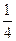 |
Eξ=
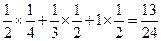
②
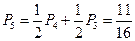
(Ⅱ)
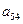 =
=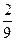
本题主要考查数列、概率、统计等基础知识,考查数据处理能力、运算求解能力,考查分类与整合思想、化归与转化思想
(Ⅰ)①ξ的可能取值为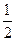 ,
,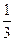 ,
,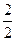
P(ξ=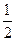 )=
)=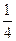 ;P(ξ=
;P(ξ= 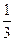 )=
)=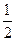 ;P(ξ=
;P(ξ= 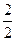 )=
)=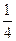 ; -------------2分
; -------------2分
ξ的分布列为
Eξ=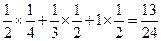 ------------
------------ -----------------------5分
-----------------------5分
②设质点移到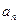 的概率为
的概率为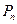 ,质点移到
,质点移到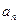 有两种可能:①质点先到
有两种可能:①质点先到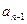 ,骰子掷出的点数为奇数,质点到达
,骰子掷出的点数为奇数,质点到达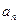 ,其概率为
,其概率为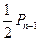 ;②质点先到
;②质点先到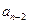 ,骰子掷出的点数为偶数,其概率为
,骰子掷出的点数为偶数,其概率为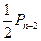 。
。
即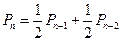 (n≥4)
(n≥4)
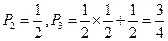
∴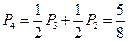
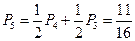 --------------------------------------10分
--------------------------------------10分
法2:质点恰好到达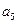 有三种情形
有三种情形
①抛掷骰子四次,出现点数全为奇数,概率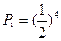 ;
;
②抛掷骰子三次,出现点数二次为奇数,一次为偶数概率为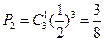 ;
;
③抛掷骰子二次,出现点数全为偶数,概度为 ,故质点恰好到达
,故质点恰好到达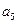 的概
的概
率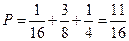 ------------------------------------10分
------------------------------------10分
(Ⅱ)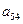 =
=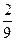 ……………………………………13分
……………………………………13分
(Ⅰ)①ξ的可能取值为
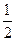 ,
,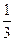 ,
,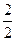
P(ξ=
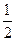 )=
)=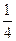 ;P(ξ=
;P(ξ= 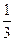 )=
)=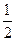 ;P(ξ=
;P(ξ= 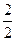 )=
)=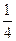 ; -------------2分
; -------------2分ξ的分布列为
| ξ | 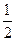 | 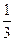 | 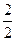 |
| P | 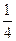 | 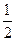 | 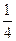 |
Eξ=
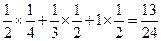 ------------
------------ -----------------------5分
-----------------------5分②设质点移到
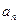 的概率为
的概率为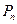 ,质点移到
,质点移到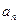 有两种可能:①质点先到
有两种可能:①质点先到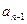 ,骰子掷出的点数为奇数,质点到达
,骰子掷出的点数为奇数,质点到达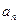 ,其概率为
,其概率为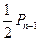 ;②质点先到
;②质点先到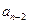 ,骰子掷出的点数为偶数,其概率为
,骰子掷出的点数为偶数,其概率为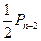 。
。即
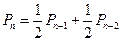 (n≥4)
(n≥4)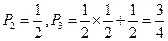
∴
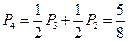
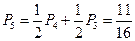 --------------------------------------10分
--------------------------------------10分法2:质点恰好到达
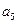 有三种情形
有三种情形①抛掷骰子四次,出现点数全为奇数,概率
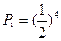 ;
;②抛掷骰子三次,出现点数二次为奇数,一次为偶数概率为
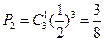 ;
;③抛掷骰子二次,出现点数全为偶数,概度为
 ,故质点恰好到达
,故质点恰好到达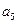 的概
的概率
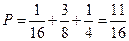 ------------------------------------10分
------------------------------------10分(Ⅱ)
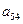 =
=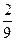 ……………………………………13分
……………………………………13分
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
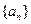 的前n项和为
的前n项和为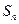 ,且
,且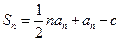 (c是常数,
(c是常数,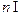 N*),
N*),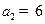 .
.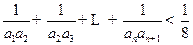 .
.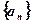 的前
的前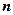 项和
项和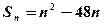 ,
,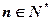 .
.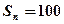 ,求
,求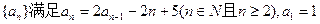
 (1)若
(1)若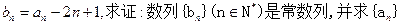 的通项;
的通项;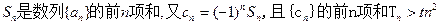 在
在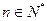 时恒成立,求实数t的取值范围。
时恒成立,求实数t的取值范围。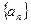 中,
中,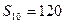 ,那么
,那么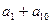 的值是 ( )
的值是 ( ) 中,
中,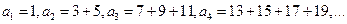 ,则
,则
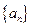 为等差数列,且
为等差数列,且 -2
-2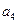 =-1,
=-1, 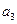 =0,则公差d=( )。
=0,则公差d=( )。
 的楼梯共有n级台阶,每步只能跨上1级或2级,走完这n 级共有
的楼梯共有n级台阶,每步只能跨上1级或2级,走完这n 级共有
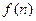 种走法,则下面各式中正确的是 ( )
种走法,则下面各式中正确的是 ( )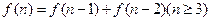
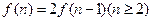
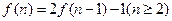
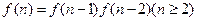
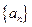 满足:
满足: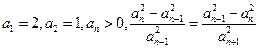
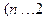 ,
,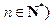 ,则
,则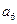 等于
等于