题目内容
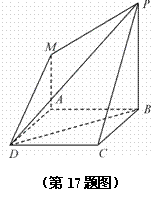
(本题满分10分)如图,四边形ABCD是正方形,PB^平面ABCD,MA^平面ABCD,
PB=AB=2MA. 求证:(1)平面AMD∥平面BPC;(2)平面PMD^平面PBD.
 |
证明:(1)∵PB^平面ABCD,MA^平面ABCD,∴PB∥MA. …………2分
∵PBÌ平面BPC,MA (/平面BPC,∴MA∥平面BPC.
同理DA∥平面BPC, …………3分
∵MAÌ平面AMD,ADÌ平面AMD,MA∩AD=A,
∴平面AMD∥平面BPC. …………5分
(2)连结AC,设AC∩BD=E,取PD中点F,连接EF,MF.
∵ABCD为正方形,∴E为BD中点.又F为PD中点,∴EF∥=PB. 又AM∥=PB,∴AM∥=EF.∴AEFM为平行四边形. …………7分
∴MF∥AE.
∵PB^平面ABCD,AEÌ平面ABCD,∴PB^AE.∴MF^PB.
因为ABCD为正方形,∴AC^BD.∴MF^BD. …………8分
又![]() ,∴MF^平面PBD. 又MFÌ平面PMD.
,∴MF^平面PBD. 又MFÌ平面PMD.
∴平面PMD^平面PBD. …………10分

 阅读快车系列答案
阅读快车系列答案
 (假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动). 的概率?
的概率? ,求
,求


 -
- 中,
中, 分别是
分别是 ,
,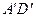 的中点,
的中点, 分别是
分别是 ,
,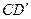 中点,
中点,

 的体积;
的体积;