题目内容
已知线段AB的两个端点A,B分别在x轴、y轴上滑动,|AB|=3,点M满足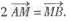
(I)求动点M的轨迹E的方程;
(II )若曲线E的所有弦都不能被直线y=k(x-1)垂直平分,求实数k的取值范围.
【答案】
解:设 ,则
,则 ,
,
由 ,得
,得 ,解得
,解得 ………………2分
………………2分
代入 ,
,
化简得点M的轨迹方程为 . …………………………5分
. …………………………5分
(2)由题意知 ,
,
假设存在弦AB被直线 垂直平分,设直线AB的方程为
垂直平分,设直线AB的方程为 ,
,
由 ,消去
,消去 化简得
化简得 ,
,
 ,
,
 ,
,
设 ,
, 中点
中点 ,
,
则 ,
………………7分
,
………………7分
 ,
,
 ,
,
又 ,
, ,得
,得 , ……9分
, ……9分
代入 ,得
,得 ,
,
解得 ,
,
因为所有弦都不能被直线 垂直平分,所以
垂直平分,所以 或
或
即实数 的取值范围是
的取值范围是 。
……12分
。
……12分
【解析】略

练习册系列答案
相关题目
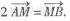
 ,点M满足
,点M满足 .
.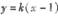 垂直平分,求实数k的取值范围.
垂直平分,求实数k的取值范围.