题目内容
为了了解某次参加知识竞赛的1252名学生的成绩，决定采用系统抽样的方法抽取一个容量为50的样本，那么总体中应随机剔除的个体数目是 ．
【答案】分析：从容量为N的总体中抽取容量为n的样本，系统抽样的前面两个步骤是：（1）将总体中的N个个体进行编号；（2）将整个编号按k分段，当 
为整数时，k=
；当 
不是整数时，从总体中剔除一些个体，使剩下的总体中的个体的个数N′能被n整除，本题中学生总数不能被容量整除，故应从总体中随机剔除个体，保证整除即可．
解答：解：学生总数不能被容量整除，根据系统抽样的方法，应从总体中随机剔除个体，保证整除．
∵1252=50×25+2，
故应从总体中随机剔除个体的数目是2，
故答案为：2．
点评：本题考查系统抽样，系统抽样的步骤，得到总数不能被容量整除时，应从总体中随机剔除个体，保证整除是解题的关键，属于基础题．
为整数时，k=；当 不是整数时，从总体中剔除一些个体，使剩下的总体中的个体的个数N′能被n整除，本题中学生总数不能被容量整除，故应从总体中随机剔除个体，保证整除即可．解答：解：学生总数不能被容量整除，根据系统抽样的方法，应从总体中随机剔除个体，保证整除．
∵1252=50×25+2，
故应从总体中随机剔除个体的数目是2，
故答案为：2．
点评：本题考查系统抽样，系统抽样的步骤，得到总数不能被容量整除时，应从总体中随机剔除个体，保证整除是解题的关键，属于基础题．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
相关题目
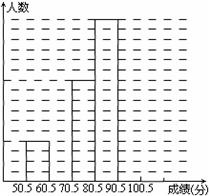为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计．请你根据尚未完成并有局部污损的频率分布表和频数分布直方图，解答下列问题：| 分组 | 频数 | 频率 |
| 50.5～60.5 | 4 | 0.08 |
| 60.5～70.5 | 0.16 | |
| 70.5～80.5 | 10 | |
| 80.5～90.5 | 16 | 0.32 |
| 90.5～100.5 | ||
| 合计 | 50 |
（Ⅱ）补全频数直方图；
（Ⅲ）学校决定成绩在75.5～85.5分的学生为二等奖，问该校获得二等奖的学生约为多少人？
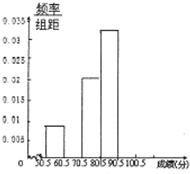某城市举行了一次“环保知识竞赛”，共有1000名学生参加了这次竞赛．为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计．请根据尚未完成的频率分布表和频率分布直方图，解答下列问题：