题目内容

10．（x+2）5的展开式中，x2的系数等于80．（用数字作答）

分析 先求出二项式展开式的通项公式，再令x的幂指数等于2，求得r的值，即可求得展开式中的x2项的系数．

解答 解：（x+2）5的展开式的通项公式为Tr+1=${C}_{5}^{r}$•x5-r•2r，
令5-r=2，求得r=3，可得展开式中x2项的系数为${C}_{5}^{3}•{2}^{3}$=80，
故答案为：80．

点评 本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，求展开式中某项的系数，属于基础题．

练习册系列答案
相关题目
20．已知非零向量$\vec a，\vec b$满足|$\vec b$|=4|$\vec a$|，且$\vec a$⊥（$2\vec a+\vec b$）则$\vec a与\vec b$的夹角为（　　）
A．$\frac{π}{3}$B．$\frac{π}{2}$C．$\frac{2π}{3}$D．$\frac{5π}{6}$
1．下列函数为奇函数的是（　　）
A．y=$\sqrt{x}$B．y=exC．y=cosxD．y=ex-e-x
18．已知函数f（x）=10$\sqrt{3}$sin$\frac{x}{2}$cos$\frac{x}{2}$+10cos2$\frac{x}{2}$．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）将函数f（x）的图象向右平移$\frac{π}{6}$个单位长度，再向下平移a（a＞0）个单位长度后得到函数g（x）的图象，且函数g（x）的 最大值为2．
（i）求函数g（x）的解析式；
（ii）证明：存在无穷多个互不相同的正整数x0，使得g（x0）＞0．
5．阅读如图所示的程序框图，运行相应的程序，则输出的结果为（　　）
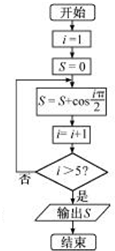
A．2B．1C．0D．-1
15．某银行规定，一张银行卡若在一天内出现3次密码尝试错误，该银行卡将被锁定，小王到银行取钱时，发现自己忘记了银行卡的密码，但是可以确定该银行卡的正确密码是他常用的6个密码之一，小王决定从中不重复地随机选择1个进行尝试．若密码正确，则结束尝试；否则继续尝试，直至该银行卡被锁定．
（1）求当天小王的该银行卡被锁定的概率；
（2）设当天小王用该银行卡尝试密码次数为X，求X的分布列和数学期望．
2．已知a＞0，b＞0，c＞0，函数f（x）=|x+a|+|x-b|+c的最小值为4．
（1）求a+b+c的值；
（2）求$\frac{1}{4}$a2+$\frac{1}{9}$b2+c2的最小值．
19．设x∈R，则“1＜x＜2”是“|x-2|＜1”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充要条件D．既不充分也不必要条件
10．已知：等差数列{an}中，a3+a4=15，a2a5=54，公差d＜0，前n项和为Sn．
（1）求数列{an}的通项公式an；
（2）求$\frac{{S}_{n}-{a}_{n}}{n}$的最大值及相应的n的值；
（3）求数列{|an|}的前n项和为Tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网