题目内容
若函数f(x)=sin ωx+ cos ωx(x∈R,ω>0)满足f(α)=-2,f(β)=0,且|α-β|的最小值为
cos ωx(x∈R,ω>0)满足f(α)=-2,f(β)=0,且|α-β|的最小值为 ,则函数f(x)的单调递增区间为________.
,则函数f(x)的单调递增区间为________.
 cos ωx(x∈R,ω>0)满足f(α)=-2,f(β)=0,且|α-β|的最小值为
cos ωx(x∈R,ω>0)满足f(α)=-2,f(β)=0,且|α-β|的最小值为 ,则函数f(x)的单调递增区间为________.
,则函数f(x)的单调递增区间为________.
f(x)=sin ωx+ cos ωx=2sin
cos ωx=2sin .因为f(α)=-2,f(β)=0,且|α-β|min=
.因为f(α)=-2,f(β)=0,且|α-β|min= ,所以
,所以 =
= ,得T=2π(T为函数f(x)的最小正周期),故ω=
,得T=2π(T为函数f(x)的最小正周期),故ω= =1,所以f(x)=2sin
=1,所以f(x)=2sin .由2kπ-
.由2kπ- ≤x+
≤x+ ≤2kπ+
≤2kπ+ ,解得2kπ-
,解得2kπ- ≤x≤2kπ+
≤x≤2kπ+ (k∈Z).所以函数f(x)的单调递增区间为
(k∈Z).所以函数f(x)的单调递增区间为 (k∈Z).
(k∈Z).
 cos ωx=2sin
cos ωx=2sin .因为f(α)=-2,f(β)=0,且|α-β|min=
.因为f(α)=-2,f(β)=0,且|α-β|min= ,所以
,所以 =
= ,得T=2π(T为函数f(x)的最小正周期),故ω=
,得T=2π(T为函数f(x)的最小正周期),故ω= =1,所以f(x)=2sin
=1,所以f(x)=2sin .由2kπ-
.由2kπ- ≤x+
≤x+ ≤2kπ+
≤2kπ+ ,解得2kπ-
,解得2kπ- ≤x≤2kπ+
≤x≤2kπ+ (k∈Z).所以函数f(x)的单调递增区间为
(k∈Z).所以函数f(x)的单调递增区间为 (k∈Z).
(k∈Z).
练习册系列答案
相关题目
 ).
).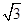 cos2x-
cos2x-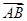 ·
·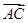 =
=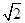 ,求△ABC的面积.
,求△ABC的面积. ),若存在a∈(0,π),使得f(x+a)=f(x-a)恒成立,则a的值是( )
),若存在a∈(0,π),使得f(x+a)=f(x-a)恒成立,则a的值是( )
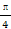

 的值域是________.
的值域是________.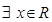 ,使
,使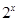 >3”的否定是“
>3”的否定是“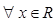 ,使
,使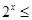 3”;
3”;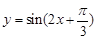 的最小正周期是
的最小正周期是 ;
;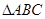 中,若
中,若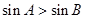 ,则
,则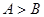 ”的逆命题是真命题;
”的逆命题是真命题;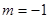 ”是“直线
”是“直线 和直线
和直线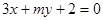 垂直”的充要
垂直”的充要
 cos x+sin x(x∈R) 的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( ).
cos x+sin x(x∈R) 的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( ).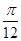



 的值域为( )
的值域为( ) ,
,