题目内容

已知数列{a_n}为等差数列，且a₁=23，公差d=-2，则其前n项和S_n达到最大值时n为

A.
10
B.
11
C.
12
D.
13

C
分析：根据数列的首项和公差，写出数列的通项公式，使得通项公式大于0，求出n的值，看出数列的n项和最大．
解答：∵a₁=23，公差d=-2
∴a_n=23-2（n-1）=-2n+25≥0，
∴n≤ $\text{[math]}$
即前12项是正数，
∴其前n项和S_n达到最大值时n为12
故选C．
点评：本题考查数列的前n项和，本题可以从不同的方面来解决，可以用通项公式来做，也可以用前n项和来解决．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

定义：在数列{a_n}中，a_n＞0且a_n≠1，若

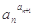为定值，则称数列{a_n}为“等幂数列”．已知数列{a_n}为“等幂数列”，且a₁=2，a₂=4，S_n为数列{a_n}的前n项和，则S₂₀₀₉=（　　）

A、6026	B、6024
C、2	D、4

定义：在数列{a_n}中，a_n＞0且a_n≠1，若anan+1为定值，则称数列{a_n}为“等幂数列”．已知数列{a_n}为“等幂数列”，且a₁=2，a₂=4，S_n为数列{a_n}的前n项和，则S₂₀₁₃等于（　　）

定义：在数列{a_n}中，a_n＞0，且a_n≠1，若anan+1为定值，则称数列{a_n}为“等幂数列”．已知数列{a_n}为“等幂数列”，且a₁=2，a₂=4，S_n为数列{a_n}的前n项和，则S₂₀₁₁等于（　　）

给出“等和数列”的定义：从第二项开始，每一项与前一项的和都等于一个常数，这样的数列叫做“等和数列”，这个常数叫做“公和”．已知数列{a_n}为等和数列，公和为

，且a₂=1，则a₂₀₀₉=（　　）

.定义：在数列{a_n}中，a_n＞0且a_n≠1，若为定值，则称数列{a_n}为“等幂数列”.已知数列{a_n}为“等幂数列”，且a₁＝2，a₂＝4，S_n为数列{a_n}的前n项和，则S₂₀₀₉＝（）A.6026 B .6024 C.2 D.4