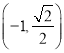题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,AB的垂直平分线分别交AB,AC于D、E(图一),沿DE将
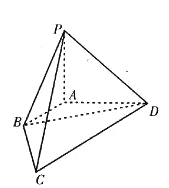
,AB的垂直平分线分别交AB,AC于D、E(图一),沿DE将![]() 折起,使得平面
折起,使得平面![]() 平面BDEC(图二).
平面BDEC(图二).

(1)若F是AB的中点,求证:![]() 平面ADE.
平面ADE.
(2)P是AC上任意一点,求证:平面![]() 平面PBE.
平面PBE.
(3)P是AC上一点,且![]() 平面PBE,求二面角
平面PBE,求二面角![]() 的大小.
的大小.
【答案】(1)见解析(2)见解析(3)![]()
【解析】
(1)取BD的中点为M,连续FM,CM,通过证明面![]() 面ADE,由此证得
面ADE,由此证得![]() 面ADE;(2)由平面几何知识可知
面ADE;(2)由平面几何知识可知![]() ,
,![]() ,平面
,平面![]() 平面BDEC,则
平面BDEC,则![]() 平面BDEC,从而
平面BDEC,从而![]() ,根据线面垂直的判定定理可知
,根据线面垂直的判定定理可知![]() 面ACD,而
面ACD,而![]() 面PBE,最后根据面面垂直的判定定理可知平面
面PBE,最后根据面面垂直的判定定理可知平面![]() 平面PBE;
平面PBE;
(3)根据(2)![]() 面ACD,设
面ACD,设![]() ,则
,则![]() ,
,![]() ,根据二面角平面角的定义可知
,根据二面角平面角的定义可知![]() 为二面角
为二面角![]() 的平面角,在三角形PQC中求出此角即可.
的平面角,在三角形PQC中求出此角即可.
(1)证明:取BD的中点为M,连续FM,CM
![]() 为AB的中点,
为AB的中点,![]() ,
,
由题知![]() 为等边三角形,
为等边三角形,![]() ,又
,又![]()
![]() ,∴面
,∴面![]() 面ADE,
面ADE,![]() 面CMF,
面CMF,![]() 面ADE
面ADE
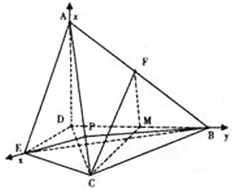
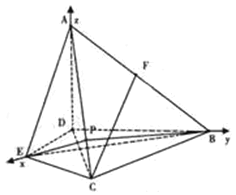
图1 图2
(2)证明:由平面几何知识:![]() ,
,![]() ,平面
,平面![]() 平面BDEC
平面BDEC
![]() 平面BDEC,
平面BDEC,![]() ,
,![]() 面ACD,
面ACD,![]() 面PBE,
面PBE,
∴平面![]() 平面PBE
平面PBE
(3)由(2)![]() 面ACD,
面ACD,
设![]() ,
,
由题意知![]() ,
,![]() ,
,
![]() 为二面角
为二面角![]() 的平面角
的平面角
![]() ,
,![]() ,
,![]() ,
,![]()
∴二面角![]() 的大小为
的大小为![]()

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目