题目内容
已知有限数列A:a1,a2,…,an,Sn为其前n项和,定义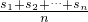 为 A的“凯森和”;如有99项的数列{a1,a2,…,a99}的“凯森和”为 1000,则有100项的数列{2,a1,a2,…,a99}的“凯森和”为
为 A的“凯森和”;如有99项的数列{a1,a2,…,a99}的“凯森和”为 1000,则有100项的数列{2,a1,a2,…,a99}的“凯森和”为
- A.991
- B.992
- C.999
- D.1001
B
分析:由题意可知S1+S2+…+Sn=na1+(n-1)a2+…+(n-2)a3+2an-1+an,由此入手,能够求出数列列2,a1,a2,…,a99的“凯森和”,即得答案.
解答:∵S1=a1,Sn=a1+a2+…+an
∴S1+S2+…+Sn=a1+(a1+a2)+(a1+a2+a3)+…+(a1+a2+…+an)
=na1+(n-1)a2+…+(n-2)a3+2an-1+an
由于数列a1,a2,…,a99的凯森和为1000
∴
∴S1+S2+…+S99=99a1+98a2+…+2a98+a99=99000
对于数列2,a1,a2,…,a99
由于S1+S2+…+S100=200+99a1+98a2+…+2a98+a99=200+99000=99200
∴ =992
=992
所以数列2、a1、a2、a3、…、a99的“凯森和”T=992.
故选B
点评:本题考查数列的性质和应用,解题时要认真审题.仔细求解,避免出错.
分析:由题意可知S1+S2+…+Sn=na1+(n-1)a2+…+(n-2)a3+2an-1+an,由此入手,能够求出数列列2,a1,a2,…,a99的“凯森和”,即得答案.
解答:∵S1=a1,Sn=a1+a2+…+an
∴S1+S2+…+Sn=a1+(a1+a2)+(a1+a2+a3)+…+(a1+a2+…+an)
=na1+(n-1)a2+…+(n-2)a3+2an-1+an
由于数列a1,a2,…,a99的凯森和为1000
∴

∴S1+S2+…+S99=99a1+98a2+…+2a98+a99=99000
对于数列2,a1,a2,…,a99
由于S1+S2+…+S100=200+99a1+98a2+…+2a98+a99=200+99000=99200
∴
 =992
=992所以数列2、a1、a2、a3、…、a99的“凯森和”T=992.
故选B
点评:本题考查数列的性质和应用,解题时要认真审题.仔细求解,避免出错.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
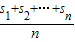 为 A的“凯森和”;如有99项的数列{a1,a2,…,a99}的“凯森和”为 1000,则有100项的数列{2,a1,a2,…,a99}的“凯森和”为( )
为 A的“凯森和”;如有99项的数列{a1,a2,…,a99}的“凯森和”为 1000,则有100项的数列{2,a1,a2,…,a99}的“凯森和”为( ) ;
; .设Sm=am+am+1+…+an,m=1,2,…,n,求证
.设Sm=am+am+1+…+an,m=1,2,…,n,求证 ,其中
,其中 表示不超过
表示不超过 的最大整数.
的最大整数.